The Material Point Method for Simulating Continuum Materials读书笔记

3 简介

MPM是结合PIC和FLIP而发展的一种算法。MPM对Lagrangian mesh连通性没有要求。

和PIC/FLIP类似，MPM算法在背景Eularian网格的辅助下，隐式处理自碰撞和破碎。与传统的Lagrangian方法（例如FEM算固体）Eularian方法（流体）相比，MPM好处如下：

和FEM一样，MPM可以由弱动量守恒形式导出，因此求解精确。
可以很容易在网格和粒子上施加边界条件、固壁碰撞和外力。
自动解决自碰撞/接触。因为粒子的运动，是由网格上未被扭曲的节点运动插值而得。
自动对物质进行分割/合并，因为物质是由粒子表示的。这对流体和颗粒状材料很有用。
只要给粒子赋不同的性质或成分模型，就能自动解决多材质和多相耦合问题。
MPM也能用于模拟基于网格的Lagrangian力，而不失其优点（见12.2节）。因此可以同时耦合用点表示的物体，和用mesh表示的物体，只需要在网格上求解一次，并能自动处理碰撞。

严格来说MPM是Lagrangian方法，但有一个Eularian网格用来算导数。坏处是拓扑结构变化、碰撞、超弹性材料效果不佳。好处是不用单独处理碰撞和拓扑结构变化。

4 MPM在工业界的应用

《冰雪奇缘》里的雪是用MPM做的。《超能陆战队》和《疯狂动物城》用到了MPM。

5 运动学理论

每个MPM粒子实际代表一个体积微元，而不是什么质点，原子之类的东西。也可以把它看作FEM里面四面体的顶点（见第9章）。

5.1 连续物质的运动

记[latex]\mathbf{X}[/latex]为“初始位置”，[latex]\mathbf{x}[/latex]为“当前位置”。初始位置集合记为[latex]\Omega^0[/latex]，当前位置集合记为[latex]\Omega^t[/latex]，它们都是[latex]R^d[/latex]的子集。[latex]\phi[/latex]是二者之间的映射关系：

物质点 [latex]\mathbf{X}[/latex] 的速度为

加速度为

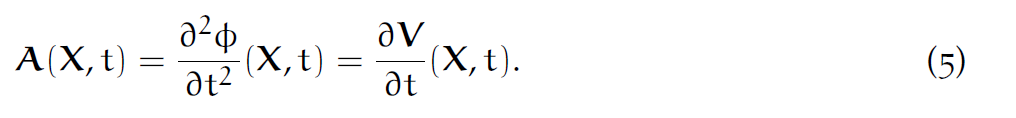
这里的速度和加速度都是以Lagrangian方式定义的，也就是说在物质点上定义的。

5.2 形变

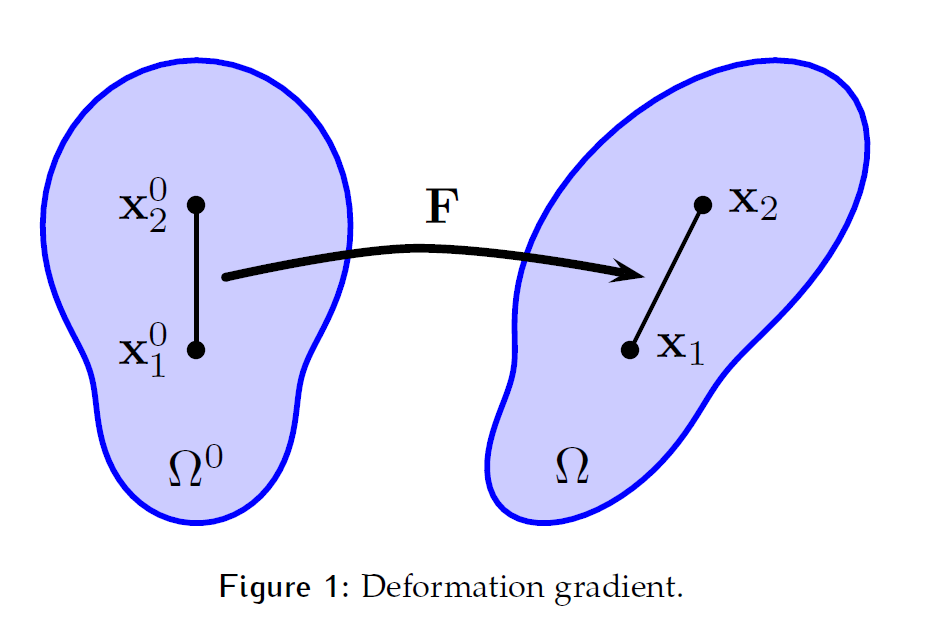
上面说的[latex]\phi[/latex]又叫做形变映射（deformation map）。它的Jacobian可以描述一些性质，比如说弹性。这个Jacobian一般记作F：

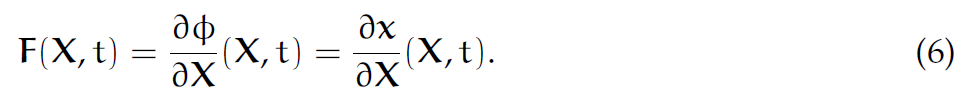
F一般简称为形变梯度（deformation gradient），也就是一个2*2或者3*3矩阵。只有一个特殊情况：对于三维布料/薄壳，F是3*2矩阵，因为材料是二维的。可以把F看作一个映射，对于某个初始点[latex]\mathbf{X}[/latex]，它的[latex]F(\mathbf{X},t)[/latex]是对应这块物质微元在时间t的形变梯度。

写开就是：

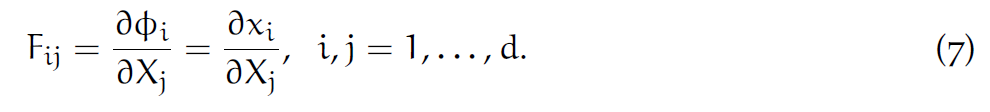
F的行列式的含义是微元的体积变化，一般把这个行列式记作J。如果J>1意味着体积增大，J<1意味着体积减小。

J=0意味着体积变为零（退化）。J<0意味着“反转”，比如一个三角形，一个顶点越过对边。第6章会讨论“invertible elasticity”模型。

5.3 前推和拉回

物质的初始状态[latex]\Omega^0[/latex]和当前状态 [latex]\Omega^t[/latex]在[latex]\phi[/latex]下同胚/微分同胚，因为 [latex]\phi[/latex] 是光滑的。 [latex]\phi[/latex] 存在一个逆映射。所以如果一个函数定义在[latex]\Omega^0[/latex]上，就可以把它给“转移”到 [latex]\Omega^t[/latex]（这叫‘前推/push forward’），当然反之也可（‘拉回/pull back’）.例如：有一个函数[latex]G: \Omega^0\rightarrow R[/latex]，可以把它前推成[latex]g(\mathbf{x},t)=G(\phi^{-1}(\mathbf{x},t))[/latex]，而g可以拉回为[latex]G(\mathbf{X})=g(\phi(\mathbf{X},t),t)[/latex].

有时把前推函数称为Eularian（定义在[latex]\mathbf{x}[/latex]上），拉回函数称为Lagrangian（定义在[latex]\mathbf{x}[/latex]上）。

速度和加速度都是Lagrangian的：

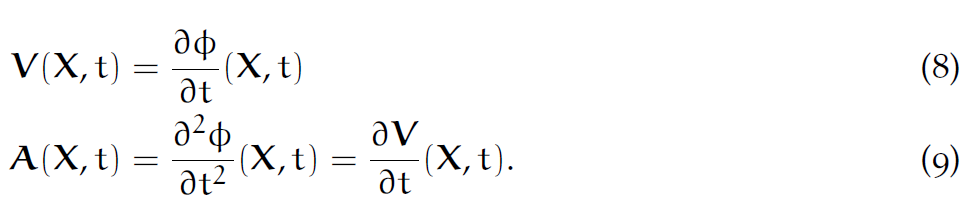
把它前推成Eularian的：

当然可以反过来写出拉回的结果：

使用a和v的定义可以写出：

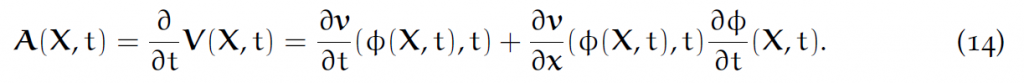
单个分量就是：

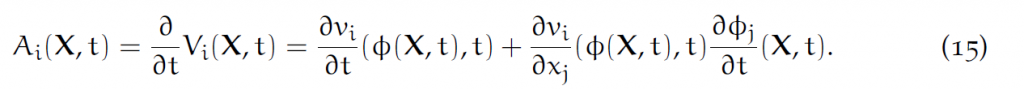
最后一项是用了爱因斯坦求和约定，代表对j=1,2,3求和。

把(8)和(10)联立，用[latex]\phi[/latex]表示Eularian速度：

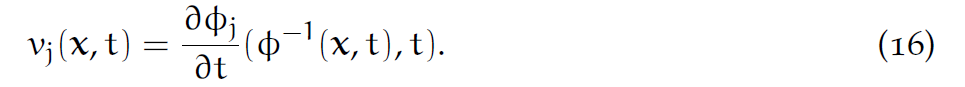
联立(11)和(15)：

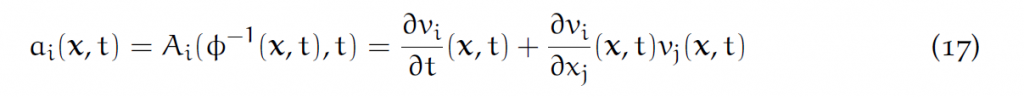
可以发现

注：这里求Lagrangian速度用的是偏导数，但是求Lagrangian加速度用了全导数，所以加速度多出来一项。也就是说，Lagrangian速度和Eularian速度相同，但加速度不同。Lagrangian加速度是速度的物质导数。

5.4 物质导数

物质导数：

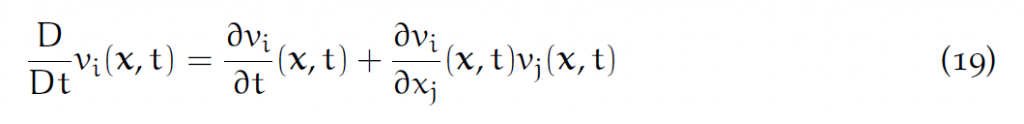
Lagrangian加速度是速度的物质导数：

对于任意Eularian函数，物质导数的定义是：

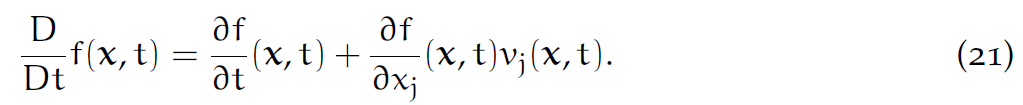
注意它是偏导数[latex]\frac{\partial}{\partial t}F[/latex]的前推。这个F是Lagrangian的，是f的拉回。这一点很重要。

形变梯度一般认为是Lagrangian的。不过也可以把它前推为Eularian的：

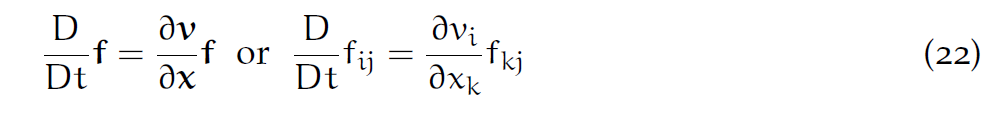
这里重复下标k代表求和。推导如下：

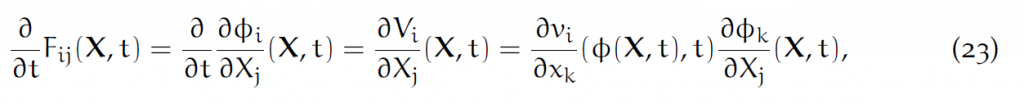
最后一步是由对(12)求导而得。

(23)式对后面求每个粒子F的离散化更新很重要（9.4节）。

5.5 体积和面积变化

初始体积微元dV在一段时间后变成了dv=JdV，其中J=det(F)。可以用三维长度推一推得到这件事情。

所以在初始物质上积分和在一段时间后物质上积分满足关系：

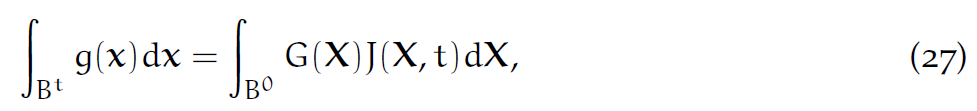
为了便于理解写成：[latex]dx=JdX[/latex].

二维有向面积：

大写S是初始状态，小写s是中间状态。

考虑一个线段微元[latex]dL[/latex]（中间状态[latex]dl[/latex]），和dS（或ds）确定一个体积：

根据上面说的[latex]dv=JdV[/latex]，所以

注意F是形变梯度。在微元内dl=FdL是对的。这对任何dL都成立。：

为什么是逆转置呢？把向量点积写成向量和向量转置相乘的形式就知道了。

如此一来，在二维表面上的积分形式如下：

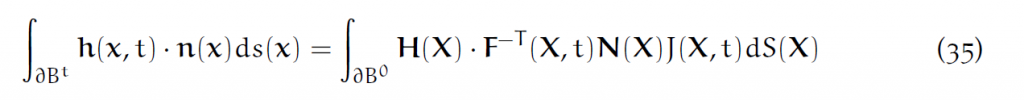
其中H是h的拉回。

6 超弹性

Stress是应力，strain是应变。

超弹性材料的第一类Piola-Kirchoff应力张量P可以由应变能量密度函数（strain energy density function）[latex]\Psi(F)[/latex]表示：

分量就是：

别忘了[latex]\Psi(F)[/latex]是弹性势能密度函数（是一个标量函数）。P和它大小相同。

在工程领域经常用Cauchy应力张量[latex]\sigma[/latex]，它和P的关系是：

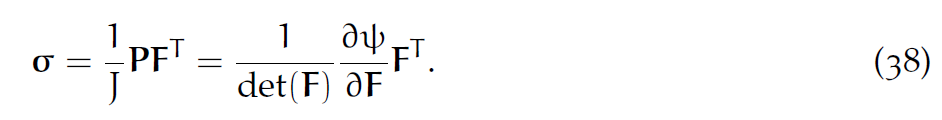
固体材料的表现就由形变映射[latex]\phi[/latex]、Cauchy应力张量 [latex]\sigma[/latex] （当然也可以用P）这两个量确定。

对于刚体而言，形变映射就是旋转加平移：

超弹性材料可以变形，但是会抵抗变形，这由[latex]\Psi[/latex]描述。注意刚体的F=R，这是一个正交矩阵。所以对于超弹性材料，当F非正交的时候，会产生应力。正交矩阵，比如R的特性是[latex]R^TR=I[/latex]，所以我们可以写成：

这样看起来较为清楚，因为正交是[latex]F^TF=I[/latex]的特殊情况，此时[latex]\tilde{\Psi}[/latex]达到最小值.这个[latex]F^TF[/latex]经常记为C（右Cauchy-Green张量）。如果材料是各向同性的，那么可以把能量写成[latex]F^TF[/latex]特征多项式的三个系数（或者叫做各向同性不变量/isotropic invariants）：

注：各向同性的意思，是不受坐标系旋转影响。也就是说乘以一个旋转矩阵结果一样。

这个结果可以简写为：

这里面[latex]F=U\Sigma V^T[/latex]是F的“Polar SVD”.这里面U和V是旋转矩阵。而F的极分解F=RS可以通过[latex]R=UV^T[/latex]和[latex]S=V\Sigma V^T[/latex]得到。这个R是距离F最近的旋转矩阵。S是对称阵。

各向同性不变量通常可以用奇异值表示。

6.2 新胡克模型

弹性势能密度函数：

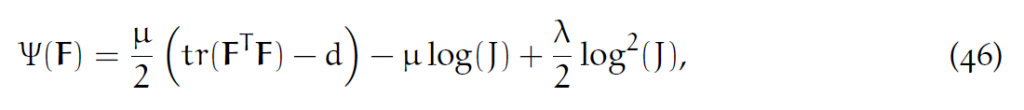
d是维度，[latex]\mu[/latex]和[latex]\lambda[/latex]由杨氏模量E、泊松比[latex]\nu[/latex]确定：

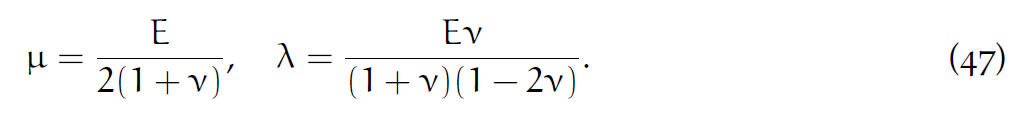
记得J是形变梯度F的行列式。如果F是旋转矩阵，[latex]\Psi=0[/latex].如果没有反转（J>0），那么[latex]\Psi(F)\geq 0[/latex].

为了计算力，需要给出P的形式：

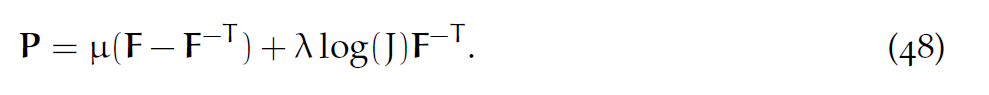
为了隐式积分，需要给出[latex]\frac{\partial P}{\partial F}[/latex]，这个在6.4节讲。

6.3 改进Corotated本构模型（Constitutive Model）

这个模型是基于SVD定义的。“改进”的意思是，它是在计算机图形学常用的corotated线性弹性模型制上进行改进。做polar SVD分解[latex]F=U\Sigma V^T[/latex]，那么改进corotated模型为：

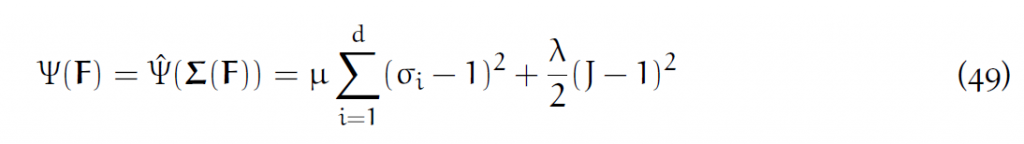
这里的[latex]\sigma_i[/latex]是SVD分解里面[latex]\Sigma[/latex]矩阵的对角元。J等于各个 [latex]\sigma_i[/latex] 之积（行列式）。把右端[latex]\mu[/latex]项展开：

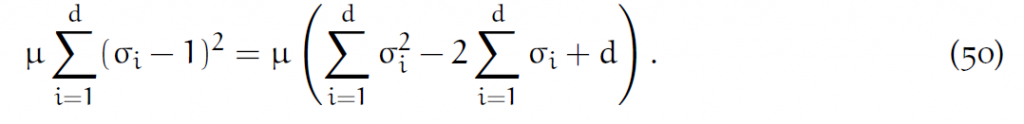
可以证明：

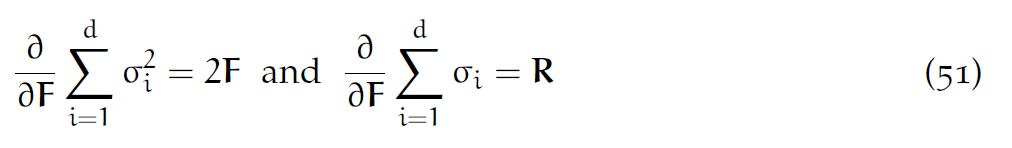
其中F=RS是极分解。给定SVD分解[latex]F=U\Sigma V^T[/latex]以后，[latex]R=UV^T[/latex]，[latex]S=V\Sigma V^T[/latex].

因此可以计算出P：

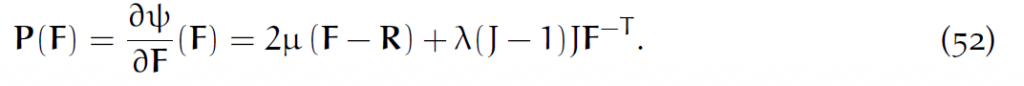
二阶导数稍微麻烦一点。

后面的太麻烦，先不管。6.4节其余部分（包括6.4.1和6.4.2）暂略。

6.5 雪的塑性（暂略）

7 物理方程

Lagrangian方程：

还记得J是形变梯度矩阵F的行列式，代表体积变化。R是Lagrangian意义下的密度。它和Eularian意义下的密度[latex]\rho[/latex]关系是：[latex]R(\mathbf{X},t)=\rho(\phi(\mathbf{X},t),t)[/latex].这个[latex]\phi[/latex]就是形变映射。注意质量守恒可以写作[latex]\frac{\partial}{\partial t}(R(\mathbf{X},t)J(\mathbf{X},t))=0[/latex].

Eularian方程：

这里v是Eularian速度，D是物质导数：[latex]\frac{D}{Dt}=\frac{\partial}{\partial t}+v\cdot\nabla^{\mathbf{x}}[/latex].

在Lagrangian方程中使用第一Piola-Kirchoff张量P更方便，在Eularian方程中则是Cauchy张量[latex]\sigma[/latex]更方便。

7.1 质量守恒

[latex]\rho(\mathbf{x},t)[/latex]是Eularian密度，R是Lagrangian密度（也就是[latex]\rho[/latex]的拉回）。二者满足关系：

Eularian密度的定义：

这个[latex]B_{\epsilon}^t[/latex]是t时刻，以[latex]\mathbf{x}[/latex]为秋心，半径为[latex]\epsilon[/latex]的球。注意这里面的体积微元实际上都是在初始状态意义上讲的。取极限就是：

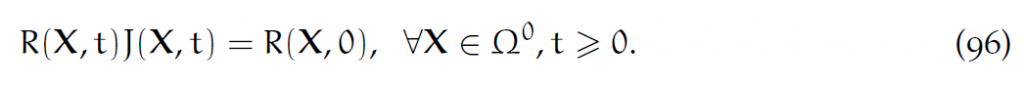
注意[latex]J(\mathbf{X},0)=1[/latex]（F是单位阵）。所以这个式子可以写成：

为了推导Eularian方程，首先把它展开：

继续展开：

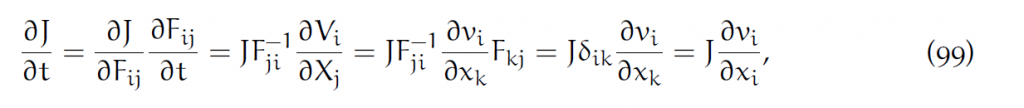
其中使用了行列式对矩阵求导的公式：

其中这个[latex]F^{-T}[/latex]的含义是[latex](F^{-1})^T[/latex].

(99)第一个等号，脚标的意思是求和。第二个等号，是考虑到F是形变梯度[latex]\phi[/latex]的Jacobian矩阵，也就是说[latex]F_{ij}=\partial\phi_i/\partial X_j[/latex].而Lagrangian速度[latex]V=\frac{\partial\phi}{\partial t}[/latex].所以这个[latex]\partial F_{ij}/\partial t[/latex]就是[latex]\partial\phi_i/(\partial t\partial X_j)=\partial V_i/\partial X_j[/latex].

第三个等号是基于5.2节的(10)式的，使用链式求导法则：[latex]\frac{\partial V_i}{\partial X_j}=\Sigma_k\frac{\partial v_i}{\partial x_k}\frac{\partial x_k}{\partial X_j}= \Sigma_k\frac{\partial v_i}{\partial x_k}F_{kj}[/latex].当然(99)中用爱因斯坦求和约定省去了求和号。

第四个等号，我们考虑其中固定i,k，对j求和的三项，会发现实际上是[latex]F^{-1}[/latex]的一列乘以F的一行，所以就是[latex]\delta_{ik}[/latex]，也就是i=k时为1，否则为0.

联立(97),(98),(99)：

这个J实际可以约掉。然后对两项都做前推。第一项的前推就是[latex]\rho[/latex]的物质导数，而R的前推就是[latex]\rho[/latex]，结果就是：

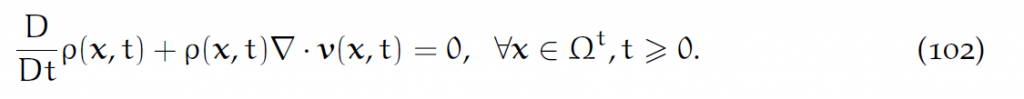
注意后面那项看起来很像物质导数的对流项，但其实不是。写开之后，实际上有三项。

7.2 动量守恒

作用在物质上的力可以分为体力（如重力）和面力（基于应力，stress-based）。

面力意味着有一个应力场（柯西应力张量）：

t是面力。

动量守恒公式：

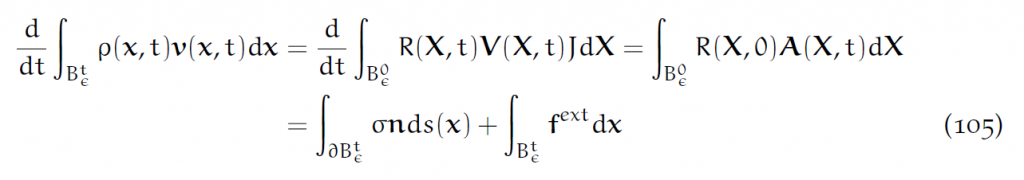
这个很好理解：体积微元内总动量的变化率等于总受力。第二个等号，用到了上面的质量守恒：[latex]R(X,t)J(X,t)=R(X,0)[/latex].

(105)的最后一个等号可以写成：

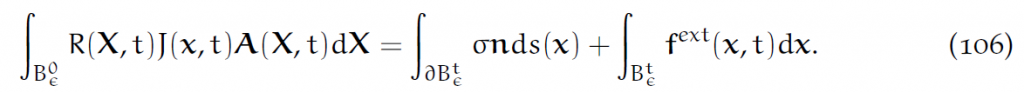
(106)左端前推：

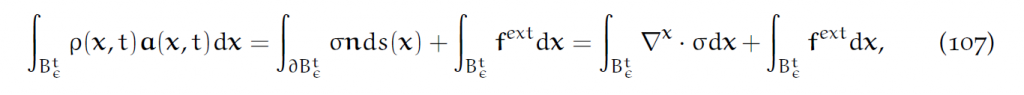
最后一个等号用了高斯公式。然后对微元取极限就是：

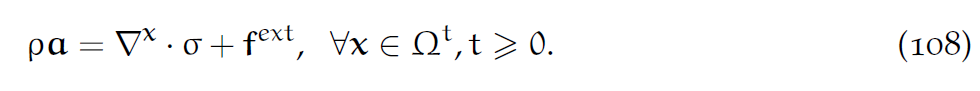
当然也可以对(106)右端做拉回。首先注意到：

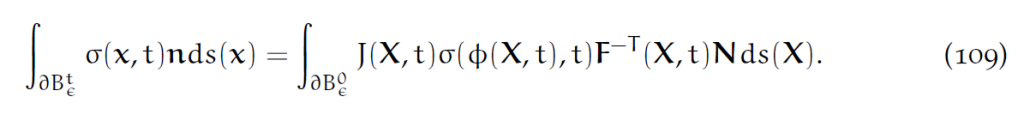
其中[latex]F^{-T}[/latex]这些是5.5节中推出来的边界积分的结果。

因为第一类Piola Kirchoff应力张量P和Cauchy应力张量的关系是[latex]P=J\sigma F^{-T}[/latex]，所以有：

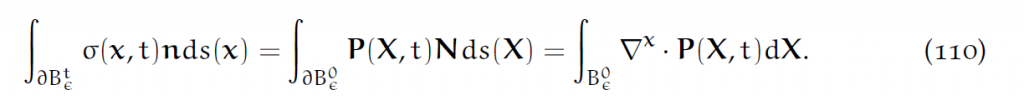
结合(106)，就得到了Lagrangian形式的动量守恒方程：

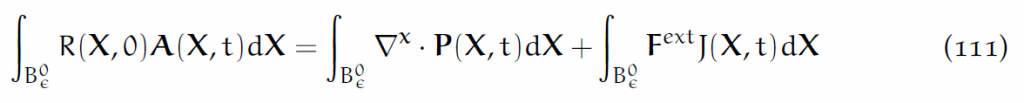
取极限：

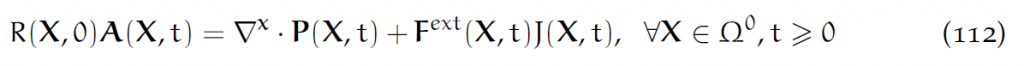
这里面的[latex]F^{ext}[/latex]是[latex]f^{ext}[/latex]的拉回。

7.3 弱形式

首先忽略外力，动量守恒方程为：

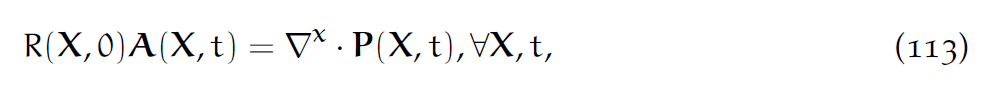
也就是：

这里[latex]R_0=R(X,0)[/latex].然后[latex]P_{ij,j}[/latex]的意思是[latex]P_{ij}[/latex]对第j坐标轴求导，当然用爱因斯坦约定隐含了对j求和。

对于任意函数[latex]Q(\cdot,t):\Omega^0\rightarrow R^d[/latex]，把它和(113)式做点积并积分起来，得到弱形式：

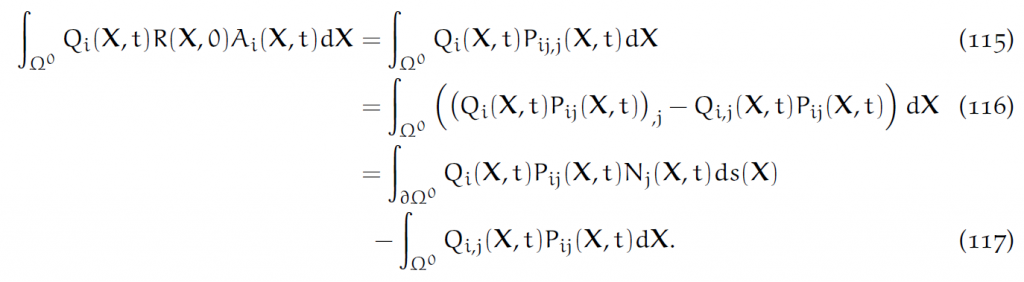
注意，这里似乎应该是只对j求和，不对i求和。

其中[latex]P_{ij}N_j[/latex]应该被作为边界条件给出。设它是T(X,t)，那么对于任意函数Q，应有：

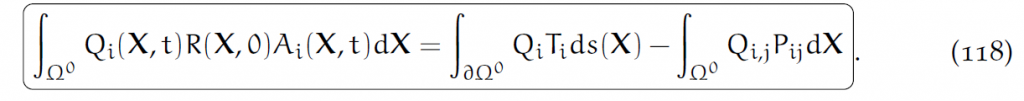
在MPM中，应力导数是在当前状态下计算的，所以可以把涉及应力的积分前推至Eularian的。令q是Q的前推，即[latex]Q(X,t)=q(\phi(X,t),t)[/latex]，反过来[latex]q(x,t)=Q(\phi^{-1}(x,t),t)[/latex]，则：

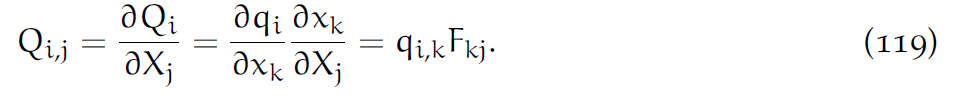
回忆起Cauchy应力张量的定义：

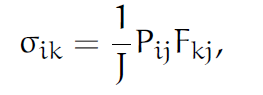
令t表示Eularian上边界的单位面积受力（即T的前推），则(118)变为：

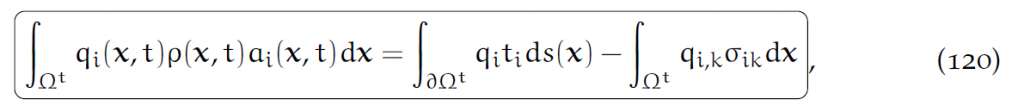
我们一项一项分析。

等号左端，[latex]\rho(x,t)J(X,t)=R(X,0)[/latex]，而[latex]dx=J(X,t)dX[/latex]，合起来就是[latex]\rho(x,t)dx=R(X,0)dX[/latex].

右端第一项，本质上就是边界受力求和，是面积上加和，至于面积变化均摊的部分实际上是算到t里面了。

右端第二项就是上面说的，Cauchy应力张量。这里应该是对k求和，而不对i求和。

(120)对任意的q都成立。我们把(120)称作Eularian下的弱受力平衡形式。MPM基于这个式子做离散化。

8 物质点

在物质点上储存质量、速度、位置。但是应力是在Eularian网格上算的，所以需要一个转移的方法。

8.1 Eularian插值函数

SPH是在粒子周围定义核函数。MPM不一样，是在Eularian格点上定义核函数（插值函数）。在格点i上定义插值函数[latex]N_i(x)[/latex]。这里的i其实应该是一个向量（原文中写的是黑体，我懒得每次mathbf了）。对于某个粒子点[latex]x_p[/latex]，常简记[latex]N_i(x_p)=w_{ip}[/latex].

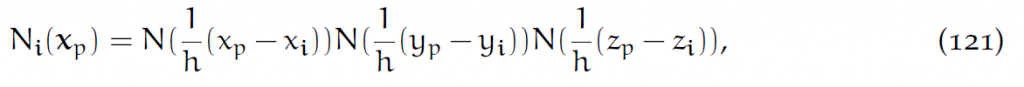
其中p是这个粒子，h是网格边长。之后简记：[latex]w_{ip}=N_i(x_p)[/latex]，[latex]\nabla w_{ip}=\nabla N_i(x_p)[/latex].

当然这里核函数N的选择很关键。我们喜欢用张量积样条（tensor product spline）.分段线性核函数对于FLIP很简单，但在这里不适用。原因有二（[Steffen et al., 2008]）：第一，如果用分段线性，[latex]\nabla w_{ip}[/latex]就不连续了，产生不连续的受力。第二，用分段线性，则在离格子远处，[latex]w_{ip}[/latex]本身很小，但[latex]\nabla w_{ip}[/latex]却很大，这不科学。MPM中使用的核函数最好具有C1连续性。二次B样条计算更快，三次B样条计算慢一些，但是效果更好。三次核函数为：

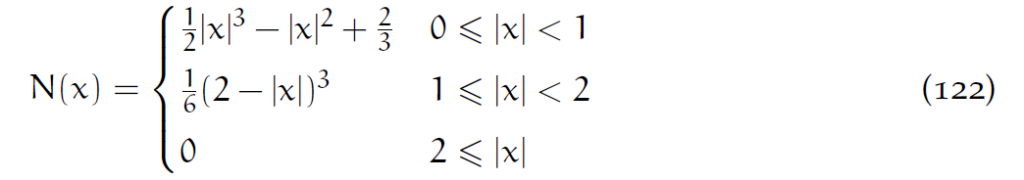
h是网格边长。二次核函数为：

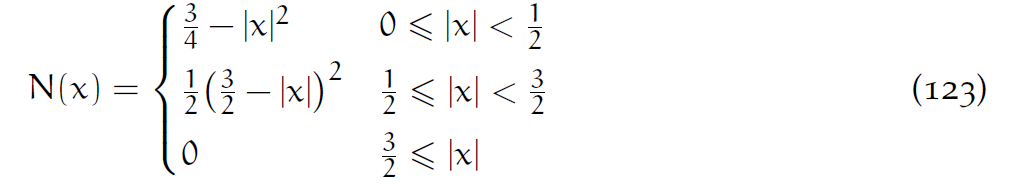
如图3所示。

虽然理论上不稳定，但某些特定情况下也可以用线性核：

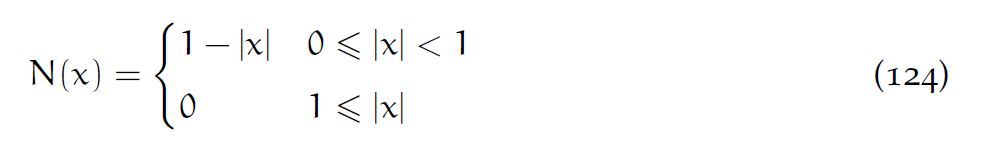
计算梯度的方法就是每一维单独算：

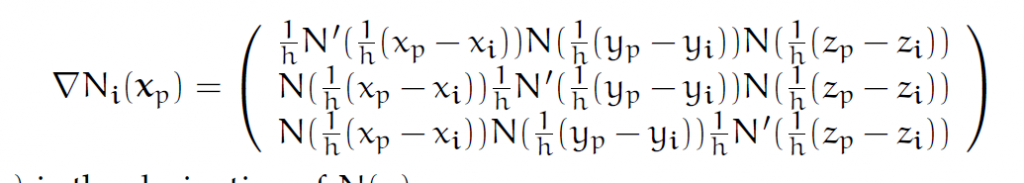
8.2 Eularian/Lagrangian质量

每个物质点代表一小块物质，质量就是这一块物质的质量。

把质量和动量（由此可以计算出能量）从物质点转移到Eularian网格上的方法就是：

[latex]m_i[/latex]就是坐标为i的网格的质量。为了质量守恒，核函数应当满足单位分解（unity partition），质量守恒率写出来如下：

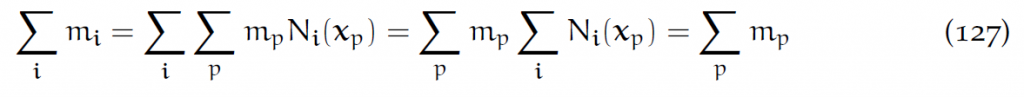
8.3 Eularian/Lagrangian动量

类似地，可以把粒子的动量[latex]m_pv_p[/latex]转移到网格上（注：我们最后实际使用10.1节所述的APIC方法）：

类似地，它同样满足守恒律：

用动量除以质量就是速度：

这里没有爱因斯坦求和约定。

把Eularian值转移到Lagrangian值的过程类似。不过不需要转移质量，因为Lagrangian质量总是不变的。速度可以通过插值得到：

动量守恒律：

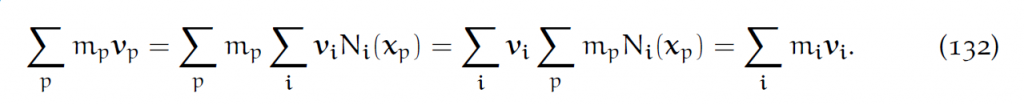
满足动量守恒律的关键一步，是由于格点质量乃从Lagrangian质量插值而得。

9 离散化

9.1 时间离散化

根据之前的弱形式：

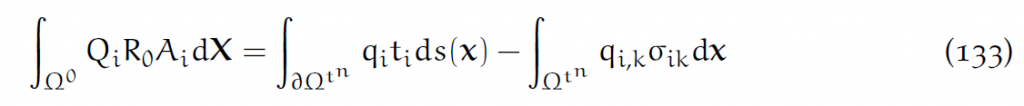
这个[latex]t^n[/latex]是当前时间步。把加速度A离散化，左端前推：

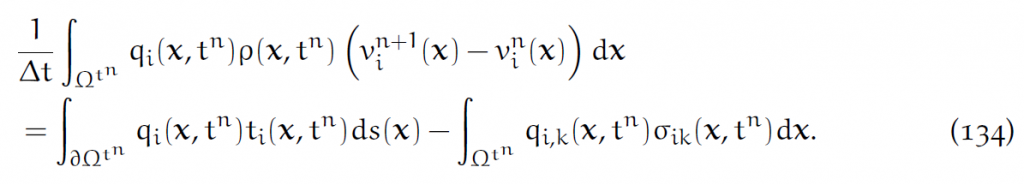
这个能成立，要记得之前说过的，[latex]\rho dx=RdX[/latex].另外式中[latex]v^n[/latex]代表第n个时间步的速度。

为了不把代表第几维的i和代表网格坐标的i混淆，接下来我们用希腊字母[latex]\alpha,\beta,\gamma[/latex]代表第几维。由此重写(134)为：

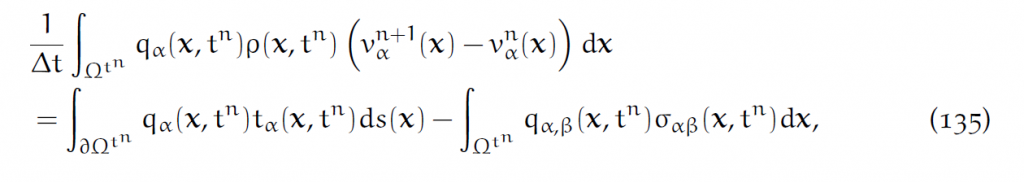
9.2 空间离散化

类似FEM，把之前的q和v都用格点插值代入：

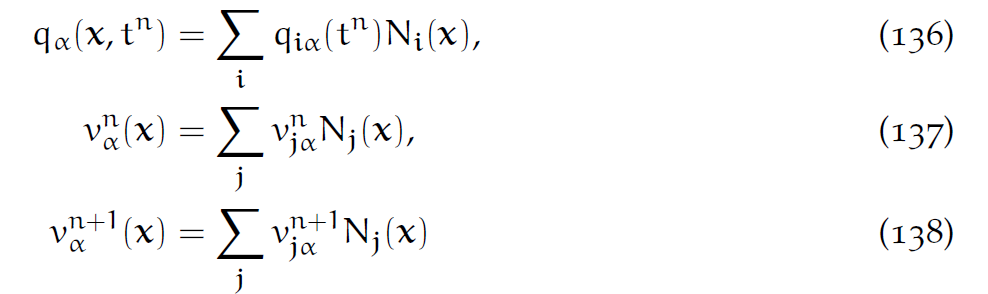
适当省略后简写为：

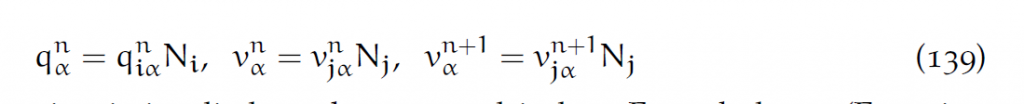
则受力平衡式(135)化为：

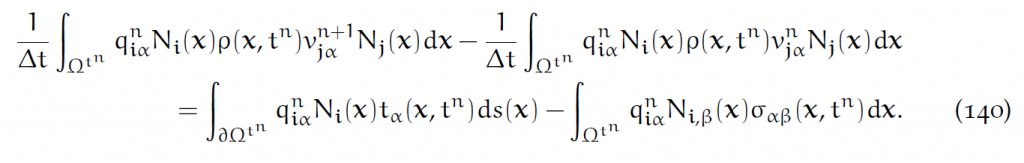
即：

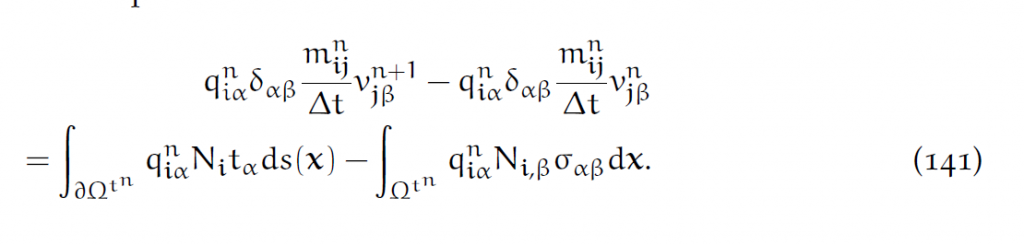
其中质量矩阵

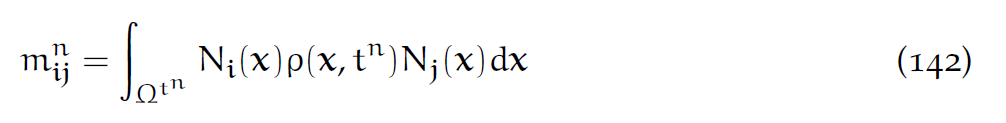
中间积分项的含义是：用格点i在x处的核函数，乘以格点j在x处的核函数。

拉回得到：

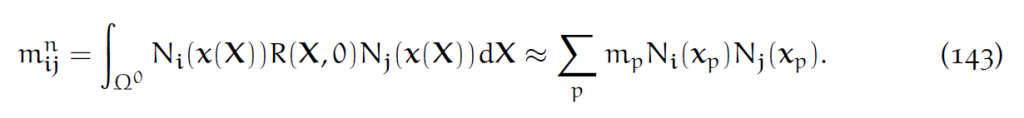
这是一个对称半正定矩阵，它可以写成[latex]BB^T[/latex]，其中[latex]B_{ip}=\sqrt{m_p}N_{ip}[/latex].但这个矩阵是奇异矩阵，我们使用mass lumping技术来构造一个正定对角矩阵来近似它。

(141)对所有q成立。我们取q为：

注意它是定义在格点上的。黑体i就是格点坐标。

则有：

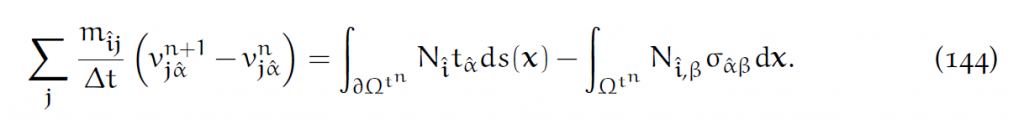
这就是离散的受力平衡方程。这个可以作为显式Eularian更新动量的方程。

经常使用mass lumping简化。方法是把[latex]m_{ij}[/latex]的每一行加起来放在对角线上。这样就是一个对角矩阵。格子i对应的行之和[latex]\hat{m_i}[/latex]就是：

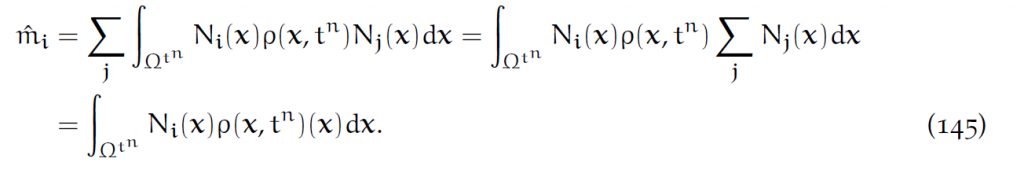
同样做简化，类似(143)：

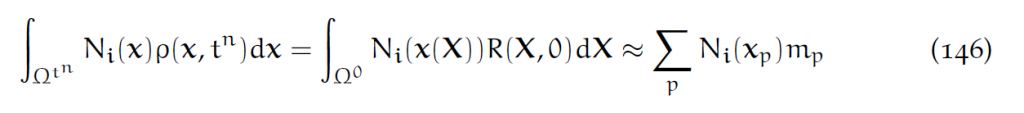
原因是[latex]m_p\approx V_p^0R(X_p,0)[/latex].也就是说[latex]\hat{m_i}[/latex]可被自然地近似为[latex]m_i[/latex].

把[latex]m_iv_i^n[/latex]写成动量[latex](mv)_i^n[/latex]，则离散方程近似为：

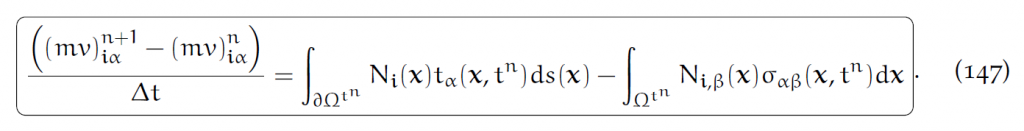
左边是动量的改变，右边近似是受力。假定我们已经对每个Lagrangian点[latex]x_p^n[/latex]计算出了张量[latex]\sigma_p^n\approx\sigma(x_p^n,t^n)[/latex]，则：

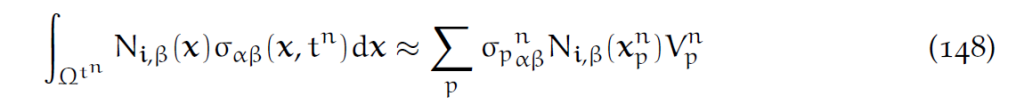
其中[latex]V_p^n[/latex]是[latex]B_{\delta x,p}^{t^n}[/latex]，也就是粒子p在时间步[latex]t^n[/latex]占的体积。

用两种方法计算[latex]V_p^n[/latex]。第一，注意到

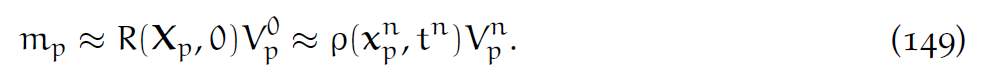
可近似估计

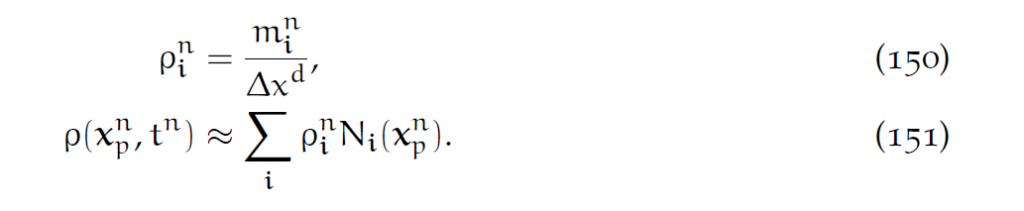
故

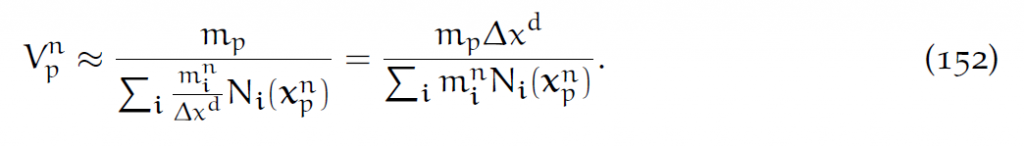
第二种方法如下。物质点p的形变梯度矩阵近似为：[latex]F_p^n\approx F(X_p,t^n)[/latex].那么其体积变化[latex]J_p^n=det(F_p^n)[/latex].假如我们知道初始体积[latex]V_p^0[/latex]，则：

使用第一类Piola Kirchoff stress：[latex]\sigma=\frac{1}{J}PF^T[/latex]，则可以把(147)和(148)中的[latex]\sigma[/latex]用P表示：

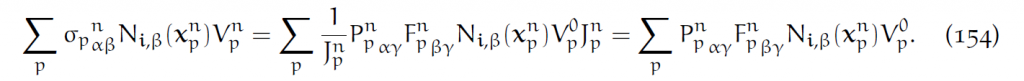
由于大部分本构模型都是指定P，所以这个写法很有用：

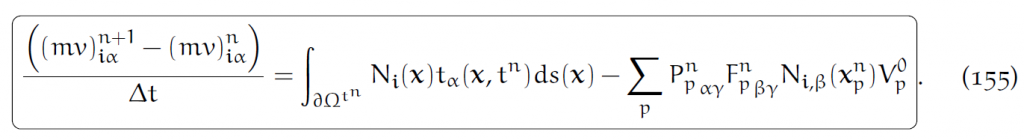
9.4 形变梯度更新

形变梯度较难计算。使用如下方程（见5.4节）：

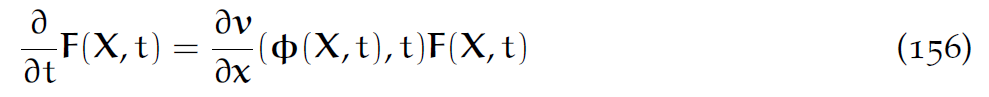
注意这个式子很神奇，把形变梯度的时间导数转换成了速度的空间导数。假设只有第n+1步的Eularian速度。则有：

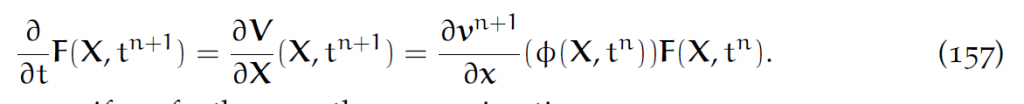
做时间离散化就是：

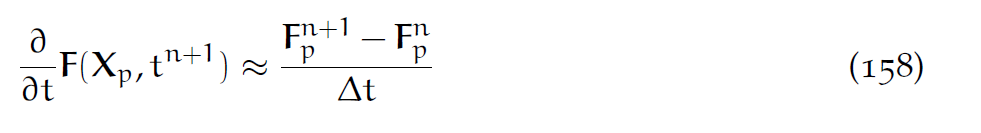
那么更新方程就是：

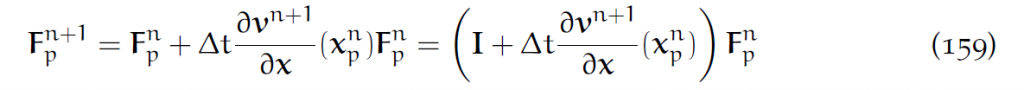
当然，把速度的插值公式写出来：

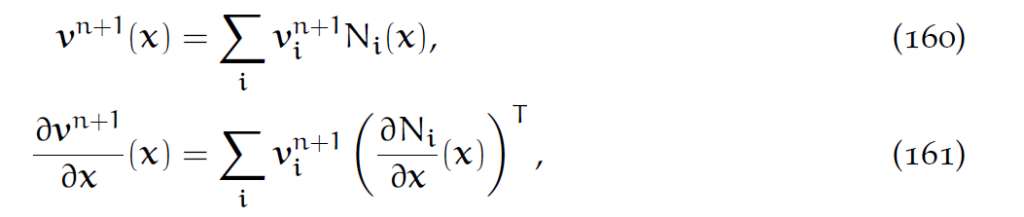
结果就是：

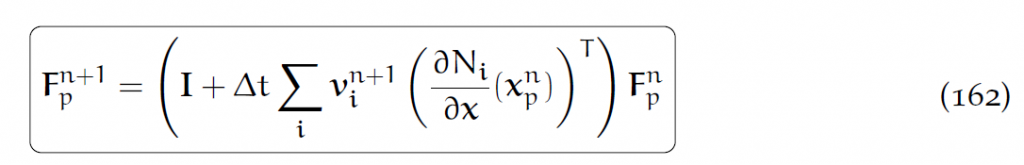
这就是给定[latex]v_i^{n+1}[/latex]和[latex]F_p^n[/latex]后更新[latex]F_p^{n+1}[/latex]的方法。

9.5 作为势能梯度的力

对于超弹性材料，第一类Piola Kirchoff应力张量由弹性势能密度定义：

如第6章所述，某节点处的弹性势能为：

其中[latex]\hat{x}[/latex]是所有Eularian格点[latex]\hat{x}_i[/latex]拼接而成的向量。这里相当于是，临时认为Eularian网格也可以动，所以用的是Eularian格点。特别地：

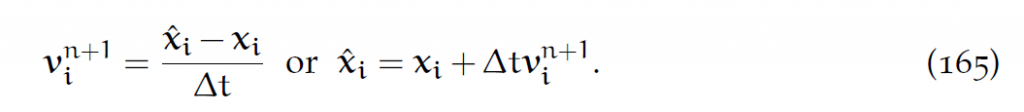
那么粒子处的形变梯度更新方式为：

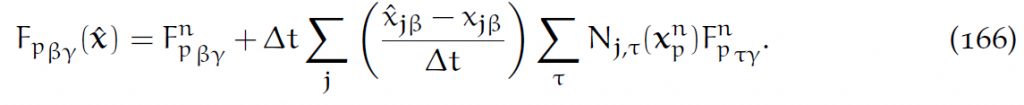
在[latex]\hat{x}_{i\alpha}[/latex]处对势能求导：

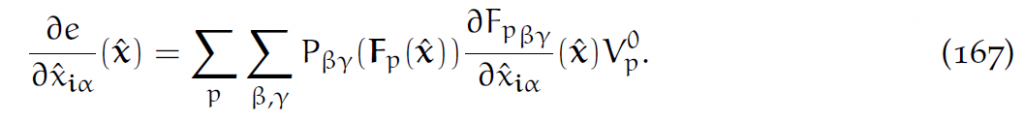
此外，根据上面F的方程，求导有：

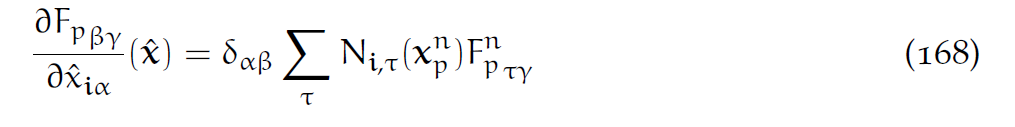
代入(167)得：

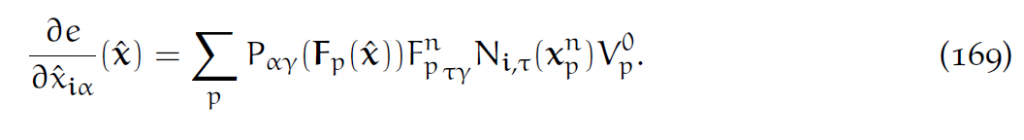
和9.3节的结果对比，发现网格受力为：

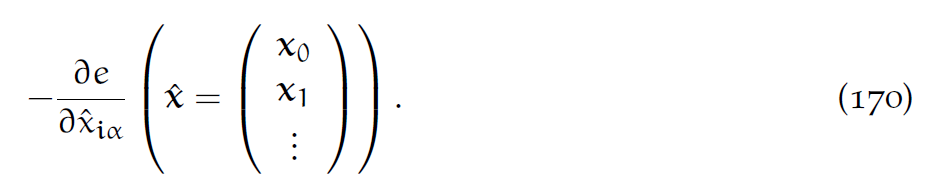
所以动量更新方程就是：

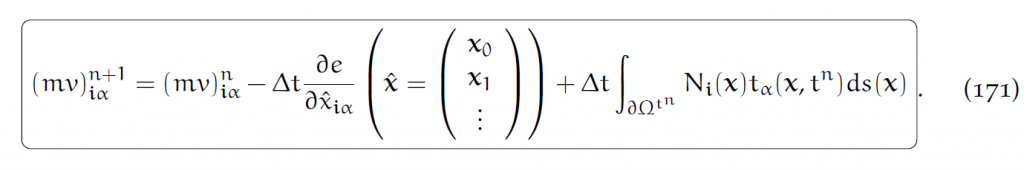
10 显式时间积分

10.1 APIC转移

可以用Affine Particle-In-Cell把物理量从粒子转移至网格。忽略代表时间的上标。

转移方程：

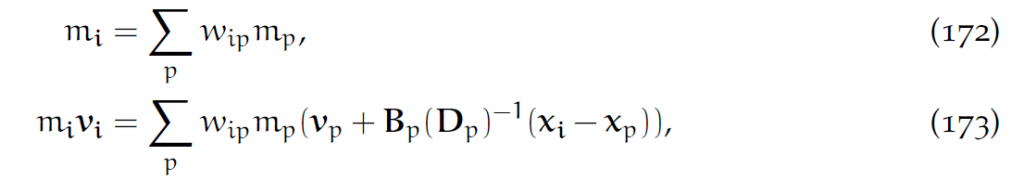
其中[latex]B_p[/latex]是存在粒子处的一个矩阵。[latex]D_p[/latex]为：

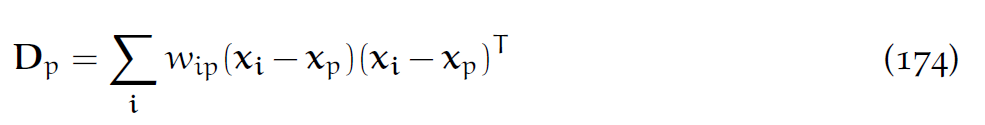
从网格转移至粒子的方程：

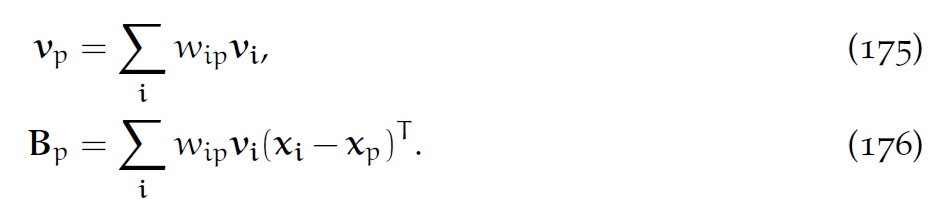
使用[latex]D_p[/latex]可以轻松表示MPM常用的二次（[latex]D_p=\frac{1}{4}\Delta x^2I[/latex]）或三次（[latex]D_p=\frac{1}{3}\Delta x^2I[/latex]）插值权值。

如果使用线性样条（虽然不推荐），为了避免[latex]D_p[/latex]成为奇异矩阵，需要改为：

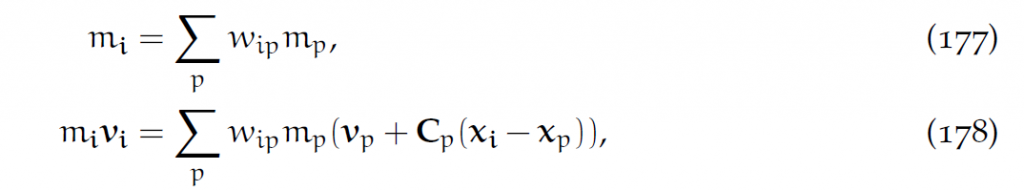
而从网格到粒子的转移方程就是：

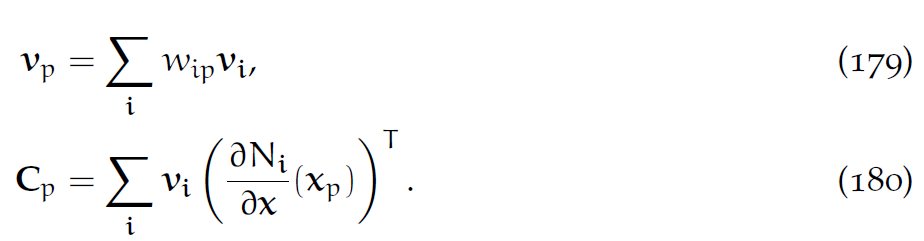
此时，[latex]C_p[/latex]是[latex]x_p[/latex]处的Eularian速度梯度。我们在更新[latex]F_p[/latex]的时候已经计算过了。

10.2 形变梯度矩阵的更新

根据网格速度场[latex]v_i^{n+1}[/latex]，则形变梯度矩阵F的更新方程为：

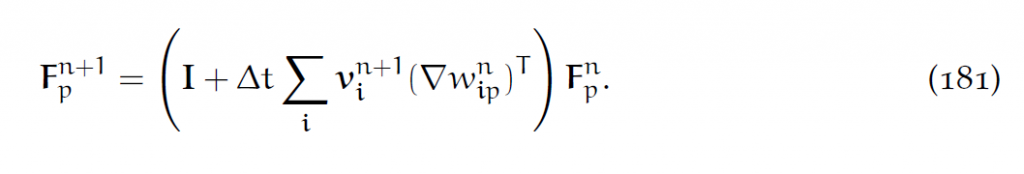
这个就是9.4节的结果。

10.3 状态更新

显式时间更新：

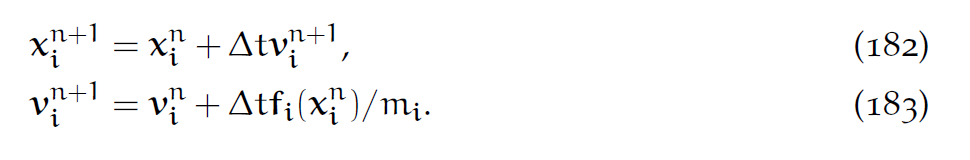
根据(182)，可以把节点位置想象成关于节点速度的函数：

那么：

即：显式的力就是假设节点没有移动时的力。使用(182)，可以把(181)重写为：

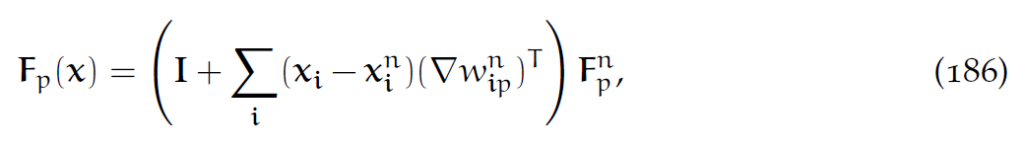
这样[latex]F_p[/latex]就是节点位置的函数。

10.4 力

MPM在格点上储存力。正如之前所述，对于超弹性固体，这个力既可以用动量守恒方程的弱形式推出，也可以用弹性势能梯度推出。后者比较简单。

首先假设我们基于网格定义了超弹性势能密度。总势能为

其中[latex]V_p^0[/latex]是粒子p的体积。

节点上的弹性力等于势能的负梯度。由(186)，形变应力为：

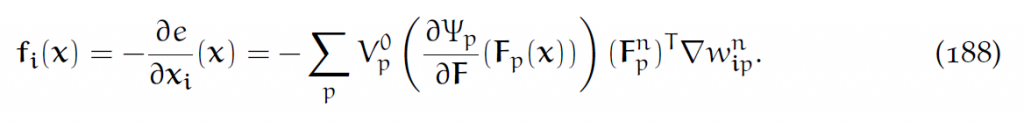
这是基于粒子计算节点处弹性力的方法。用辛Euler方程，可以写成：

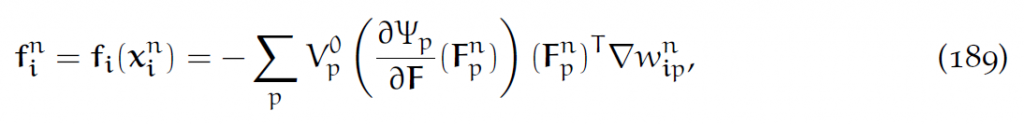
完全取决于已有的插值权值，以及粒子的物理量。如果不用能量密度，也可以用Cauchy应力张量表示这个力：

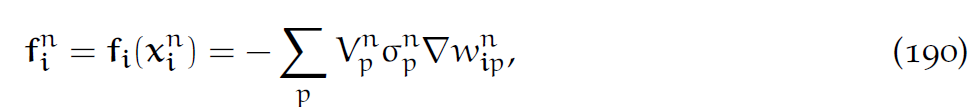
10.5 MPM整体流程

下面描述基于辛Euler方法的MPM。假设已经初始化了所有粒子（赋予质量[latex]m_p[/latex]，体积[latex]V_p^0[/latex]，初始位置[latex]x_p[/latex]，初速度[latex]v_p[/latex]，仿射矩阵[latex]B_p[/latex]和其他材料相关参数）。

物理量从粒子转移至网格(Particle to Grid, P2G)。使用10.1节所述的APIC公式，把粒子上的物理量（即：质量和动量）转移至网格上。
计算格点速度。[latex]v_i=\frac{m_iv_i}{m_i}[/latex]。对于质量为0的格点，把速度设为0.一般认为会在这种地方设置浮点数阈值，用来避免除以零。不过其实直接和浮点数0.0f相比也没什么问题，因为就算质量很小，导致除法运算得到一个很大的速度，但最后向粒子转移的时候，也要被这个质量再放缩回去。实际上在这里设置浮点阈值反而有害，会导致总动量不守恒之类的问题。
确定自由度。这一步对于效率很关键。把质量非零的格点标记出来。其他节点没有自由度，保持不变，不在求解器中作为未知量出现。
使用(189)式，显式计算格点上的力[latex]f_i^n[/latex]。
使用(183) 式更新网格速度。这一不需要考虑边界条件和物体碰撞。对于显式积分而言，每个格点处的速度都可以被Dirichlet边界条件，或者刚体碰撞来单独设置。处理碰撞的细节具体见12.1节。
使用(181)式更新粒子的形变梯度。注意我们并不实际把格点移到计算出来的新的位置，这只是一种假设，用来计算速度。
把物理量从网格转移至粒子。这一步使用10.1节所述方法，计算出新的粒子速度[latex]v_p^{n+1}[/latex]和新的仿射矩阵[latex]B_p^{n+1}[/latex]。
粒子advection。基于速度advect粒子：[latex]x_p^{n+1}=x_p^n+\Delta tv_p^{n+1}[/latex]。注意只有APIC是这么advect的。在FLIP或者混合PIC/FLIP方法中，advect方程是[latex]x_p^{n+1}=\Sigma_ix_i^{n+1}w_{ip}[/latex]。（对于PIC或者APIC，这两个式子相同）。

11 隐式积分

隐式和显式的主要区别是更新网格速度场。

11.1 力的导数

总的弹性势能可以由势能密度积分而得：

对应力做空间离散化，等于在格点上对这个势能密度做离散近似，然后求导。当然，我们并不真正改变格点的位置。设格点i的位置是[latex]x_i[/latex]，那么它下一步“应该”在的位置是[latex]\hat{x_i}=x_i+\Delta tv_i[/latex]，为简单起见，略去下标i，那么总势能就是：

这个[latex]V_p^0[/latex]就是粒子p初始时占据的体积，[latex]\hat{F}_p[/latex]为：

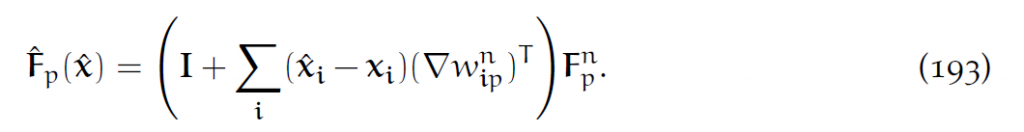
那么应力离散化为：

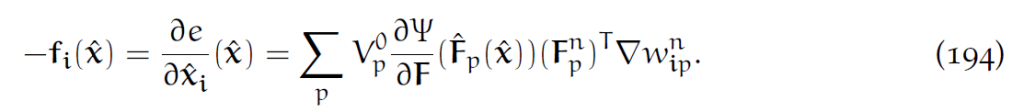
这个[latex]f_i(\hat{x})[/latex]就是格点i的弹性力。写成Cauchy应力张量[latex]\sigma_p=\frac{1}{J_p^n}\frac{\partial\Psi}{\partial F}(\hat{F_p(\hat{x})})(F_p^n)^T[/latex]：

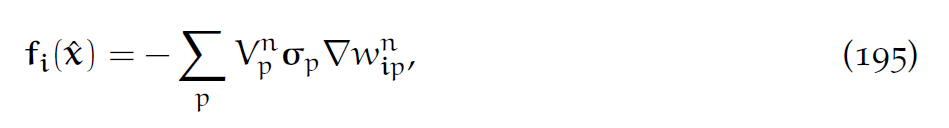
这个[latex]V_p^n=J_p^nV_p^0[/latex]，就是时间步n时粒子p的体积。

我们使用势能的Hessian矩阵来做隐式更新。对于任意小扰动[latex]\delta u[/latex]的Hessian矩阵为：

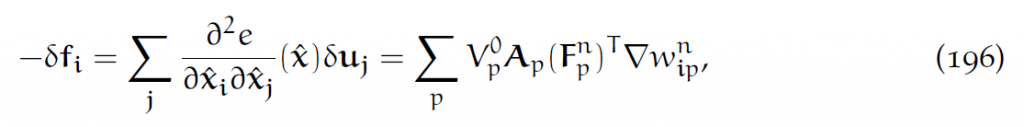
其中

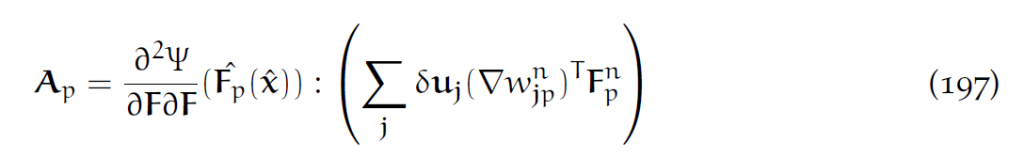
这里面冒号的含义是：A=C:D意味着[latex]A_{ij}=C_{ijkl}D_{kl}[/latex]（隐含对kl的求和）。

也可以用格点的方式推导。注意这个力在(188)中已经被推导出来，求导有：

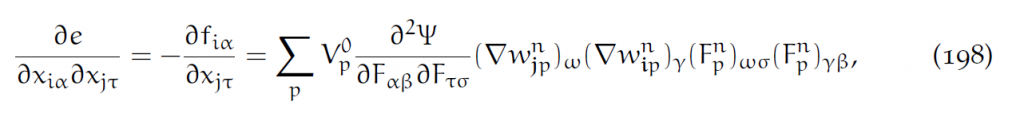
其中[latex]\frac{\partial^2\Psi}{\partial F^2}[/latex]可以由[latex]\Psi(F)[/latex]导出。

11.2 反向Euler系统

和(183)式（[latex]v_i^{n+1}=v_i^n+\Delta tf_i(x_i^n)/m_i[/latex]）不同，反向Euler的更新方式为：

其实就是把第n步的受力换成了第n+1步的受力。也就是说，受力会隐式地依赖于网格的运动。这允许我们把时间步变得更大。

重排后得到一个非线性的格点速度公式：

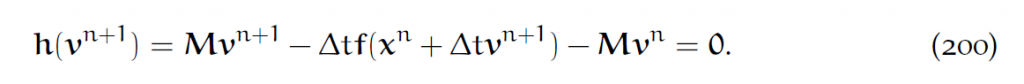
11.3 牛顿法

可以用牛顿法解(200)式。初始猜测可以取上一步的速度。然后迭代步为：

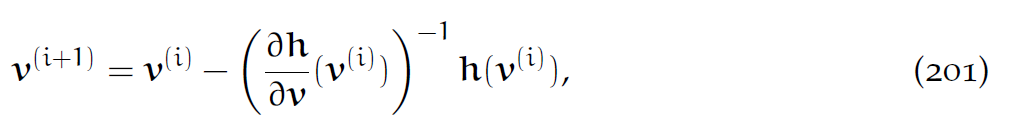
每一步都是求解一个线性系统，这可以用诸如MINRES的Krylov求解器。在牛顿迭代中，[latex]F_p[/latex]需要根据速度更新。需要储存上一个时间步的[latex]F_p^n[/latex]，以备迭代使用。

在许多情况下，只需要做一步牛顿迭代，效果就非常好，能以比显式方法多出数量级的时间步做到相同效果。这几乎和所谓“半隐式”MPM积分效果相同。

11.4 线性力

弹塑性响应可以由网格位置的虚拟“更新”确定。把这种虚拟更新写成[latex]\hat{x}[/latex]关于v的函数：[latex]\hat{x}=\hat{x}(v)[/latex]。我们使用如下记号：[latex]f_i^n=f_i(\hat{x}(0))[/latex]，[latex]f_i^{n+1}=f_i(\hat{x}(v_{n+1}))[/latex]，[latex]\frac{\partial^2 e^n}{\partial\hat{x}_i\hat{x}_j}=-\frac{\partial f_i^n}{\partial \hat{x}_j}=-\frac{\partial f_i}{\partial \hat{x}_j}(\hat{x}(0))[/latex].

由此写出隐式速度更新：[latex]v_i^{n+1}=v_i^n+\Delta tm_i^{-1}((1-\beta)f_i^n+\beta f_i^{n+1})=\approx v_i^n+\Delta tm_i^{-1}(f_i^n+\beta\Delta t\Sigma_j\frac{\partial f_i^n}{\partial \hat{x}_j}v_j^{n+1})[/latex].这是一个求解[latex]v_i^{n+1}[/latex] 的对称方程组：

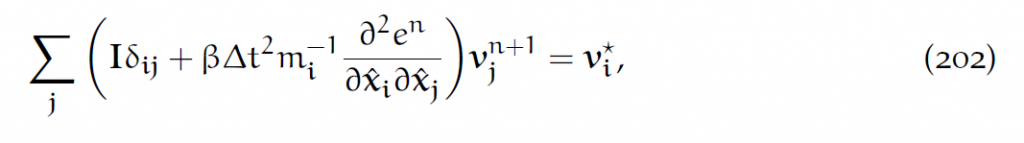
其右端就是：

参数[latex]\beta[/latex]取0时就是显式，取0.5时就是梯形公式，取1就是反向欧拉。这相当于以全0场为初值，做一次牛顿迭代。因此，这样每步只需要解一个线性系统。MPM半隐式时间步见图4。

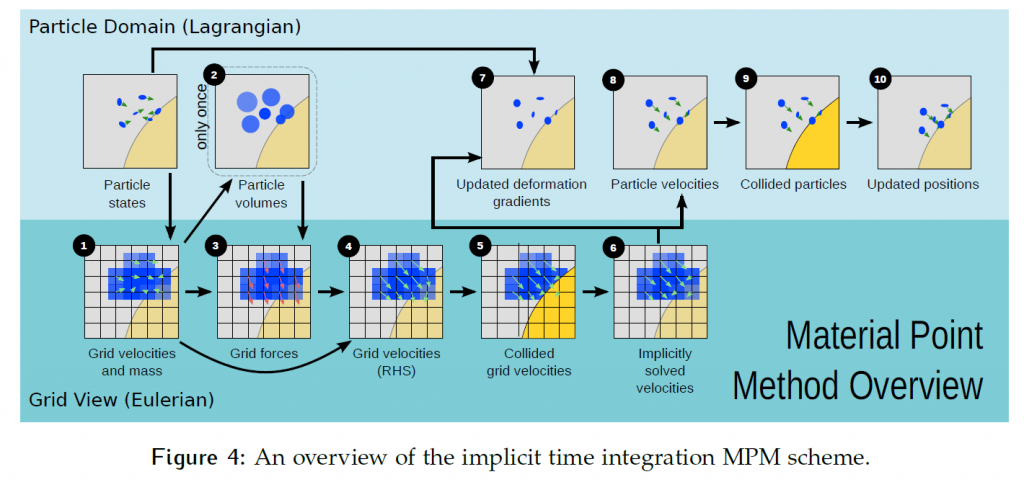
11.5 基于优化的时间积分

Newton-Raphson求解器性能比显式时间步好得多，但仍然需要较小的时间步才能达到稳定。

如果力是由势能函数得到的（这在大多时候成立），那么就可以让牛顿法在和CFL条件相近的任意[latex]\Delta t[/latex]内收敛，方法是把远方程写成一个优化方程。

实际上，求解：

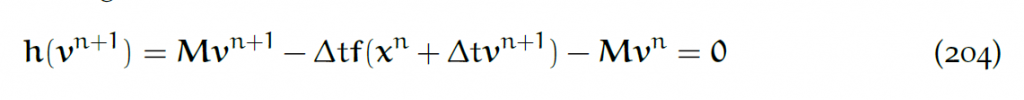
等价于最小化：

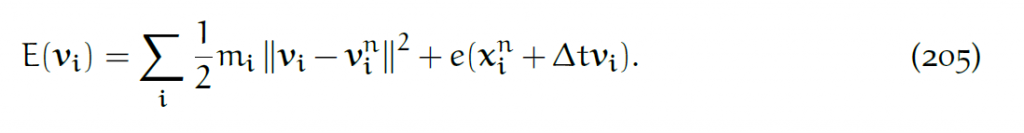
这允许我们采取大得多的时间步，节省大量运算资源。具体情况见[Gast et al., 2015].

12 其他

12.1 物体碰撞

在使用受力更新网格速度后，我们就处理碰撞问题。对于半隐式积分，这涉及到修改线性方程组的右端，并且消除涉及到碰撞的格点的自由度。可以在更新粒子坐标之前，对粒子速度[latex]v_p^{n+1}[/latex]做一次碰撞检测，用来解决插值引入的新误差。所有碰撞都是非弹性的。注意基于粒子的碰撞会让粒子上的形变梯度张量自相矛盾。因此在模拟中，只应该在必要情况下使用这种碰撞。

我们使用level set表示碰撞的物体。那么碰撞检测就很简单（[latex]\phi\leq 0[/latex]）。首先计算出相对速度[latex]v_{rel}=v-v_{co}[/latex]，这个co是碰撞物体的意思。如果两个物体互相分离，那么不加碰撞。记[latex]v_t=v_{rel}-nv_n[/latex]为相对速度的切向分量。如果需要一个“sticking impulse”（[latex]||v_t||\leq-\mu v_n[/latex]），那么直接设[latex]v’_{rel}=0[/latex]，这个撇代表已经处理过碰撞了。否则就用使用动态摩擦，更新为[latex]v’_{rel}=v_t+\mu v_nv_t/||v_t||[/latex]，其中[latex]\mu[/latex]是摩擦系数。最后基于相对速度去更新速度：[latex]v’=v’_{rel}+v_{co}[/latex].

我们有两种碰撞物体：刚体和软体。刚体就储存一个固定的level set，和刚体的位置参数，用来计算每个点的[latex]\phi[/latex]，法向和物体速度。对于软体，在关键帧加载level set，并使用[latex]\phi(x,t+\gamma\Delta t)=(1-\gamma)\phi(x-\gamma\Delta tv_{co},t)+\gamma\phi(x+(1-\gamma)\Delta tv_{co},t+\Delta t)[/latex]做时间插值。但速度则用[latex]v_{co}=(1-\gamma)v(x,t)+\gamma v(x,t+\Delta t)[/latex]，忽略位置变化。

最后考虑粘性碰撞。此时Coulomb摩擦是不够的，因为法向相对速度应该是0（垂直）或者正数（悬挂在下面，然后由于重力又分开）。这里我们无条件地设置[latex]v’_{rel}=0[/latex]。也就是说，这等价于Dirichlet边界条件。

12.2 Lagrangian力

在传统MPM模拟中，使用(188)式计算力。在粒子处储存形变梯度有一定好处，例如不用考虑拓扑。但是在用MPM模拟传统的软体，比如橡胶之类的东西时，使用基于mesh的FEM求解器更有道理，因为它提供了连通性信息，能更精确地计算形变梯度矩阵，并且有利渲染。在此情况下，MPM可以和基于mesh的方法轻松整合在一起。

我们可以使用任何Lagrangian受力模型（例如弹簧，有限元等等），只要能写出每个点处的总势能[latex]W(x_p)[/latex]。基于这个模型计算出受力[latex]f_p=-\frac{\partial W}{\partial x_p}[/latex]。设对于任何粒子处的位移[latex]\delta u_q[/latex]，都可以计算相应受力[latex]\delta f_p=\Sigma q\frac{\partial f_p}{\partial x_q}\delta u_q[/latex].这些是纯Lagrangian的，可以用常规方法做，我们就不详述了。

然后考虑如何把它们加到网格上。我们需要根据粒子处的受力[latex]f_p[/latex]计算处网格受力[latex]f_i[/latex]，并根据[latex]\delta u_i[/latex]计算[latex]\delta f_i[/latex]。考虑之前粒子-网格之间互相转移的方法，我们得到[latex]x_p=\Sigma i w_{ip}^nx_i[/latex].使用链式法则：

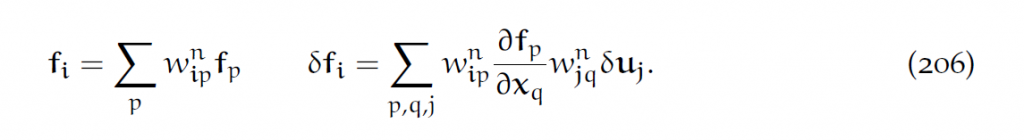
这里有三个隐含求和，不过计算起来并不难，可以一个一个做。这些是网格上的受力，那么MPM和Lagrangian方法就可以整合起来。把每个粒子标记为MPM粒子或者是mesh粒子。我们不会使用储存在mesh粒子上的形变梯度矩阵，因为直接在mesh上计算即可。这就能把Lagrangian方法的精确表面追踪和Eularian网格的自动处理碰撞给结合在了一起。