参考文献:Interface reconstruction with least-squares fit and split advection in three-dimensional Cartesian geometry
在流体模拟中,我们可以用VOF(volume of fluid,体积分数)方法追踪两相之间的界面。而VOF场的演化需要对流,做这种对流的最佳方案之一是用所谓的piecewise linear方法,即在每个格子内部估计一个平面作为局部界面,在对流时根据这个界面计算通过格子之间界面的物质通量。
而在这种方法当中,想要估计平面,需要先计算出这个平面的法向,然后再确定其截距。本文所描述的Mixed Youngs-centered格式就是一种根据VOF场估计法向的方法。
结果判据
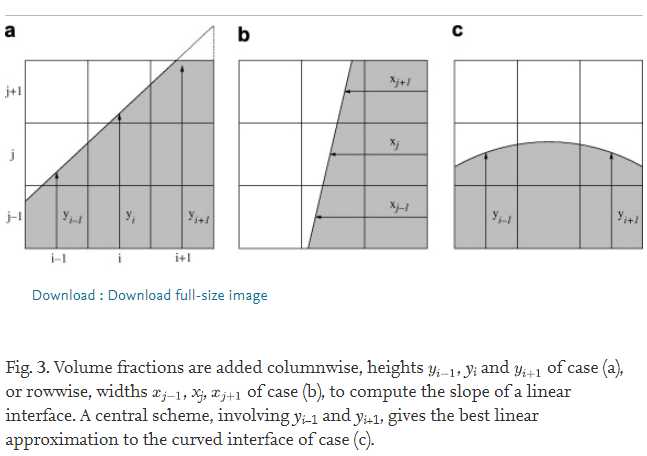
观察如下图(图3)所示的一个3*3二维区域,其中格子边长为h.
可以在每一行把体积分数加起来,得到一个局部的高度函数y=f(x),或者在每一列把体积分数加起来,得到一个局部的宽度函数x=g(y).
而需要估计的平面,在这种二维情况下是一条直线\mathrm{sgn}(m_y)y=m_xx+\alpha’. 为什么要加sgn?因为这种高度函数无法区分水在上还是空气在上。
例如图a中的情景,我们可以对f(x)求导来计算斜率。这时就有一个问题:是用前向差分,后向差分还是中心差分呢?对于这张图而言,用i-1和i计算i处的斜率,能给出正确结果,因为界面穿过了i-1和i列的左右两条边,因此其高度函数f(x)反映的是真实的VOF。但如果用i和i+1计算这个斜率,就会出现问题,因为界面穿过了i+1列的左边和上边,因此i+1列的高度函数并未完全反映其VOF值,而是欠缺了一部分(即图3.a中右上角多出的白色小角)。此时,这种前向差分所计算出的斜率将比真实值更平缓。
这样我们就获得了一个判据,即如果对某个斜率m_x有两种估计m_{x1},m_{x2},我们应当选择其中绝对值较大的那个:
|m^*|=\max(|m_{x1},m_{x2}|).
类似地,我们也可以用宽度函数g(y)估计另一种定义下的斜率m_y,此时方程为\mathrm{sgn}(m_x)x=m_yy+\alpha^{”}.何时用m_x,何时用m_y呢?对比图3.a和图3.b,我们发现如果用f(x)计算图3.b的斜率,这个斜率会非常大(例如,第一列的VOF为0,而第三列的VOF就陡升至3)。也就是说,界面为横向时,m_x的绝对值较小,此时应当用m_x,而界面为纵向时,m_y的绝对值较小,应当用m_y。这可以总结成如下公式,即在x和y之间应当选择绝对值较小的那个:
|m^*|=\min(|m_{x1},m_{y1}|).
需要指出的是,这个判据有时候也会失灵,比如图3.c的情况,此时最好的估计是f'(x)=0,但这个结果恰恰是m_x当中绝对值最小的那个,而非最大。
本文将把这两个判据扩展至三维,三维中的平面方程将形如\mathrm{sgn}(m_z)z=m_xx+m_yy+\alpha。根据二维判据的想法,我们应当检查|m_x|+|m_y|,但为了方便起见,计算时会将(\mathrm{sgn}(m_z),m_x,m_y)给normalize到绝对值之和为1,记作(m_z^0,m_x’,m_y’)。那么这时其实只用检查m_z^0,但最小化就改成了最大化,即:
|m^*|=\min(|m_{z1}^0|,m_{z2}^0).
同样,不同轴的选取也要相应改变:
|m^*|=\max(|m_{z1}^0|,|m_{y1}^0|).
Mixed Youngs-Centered Scheme
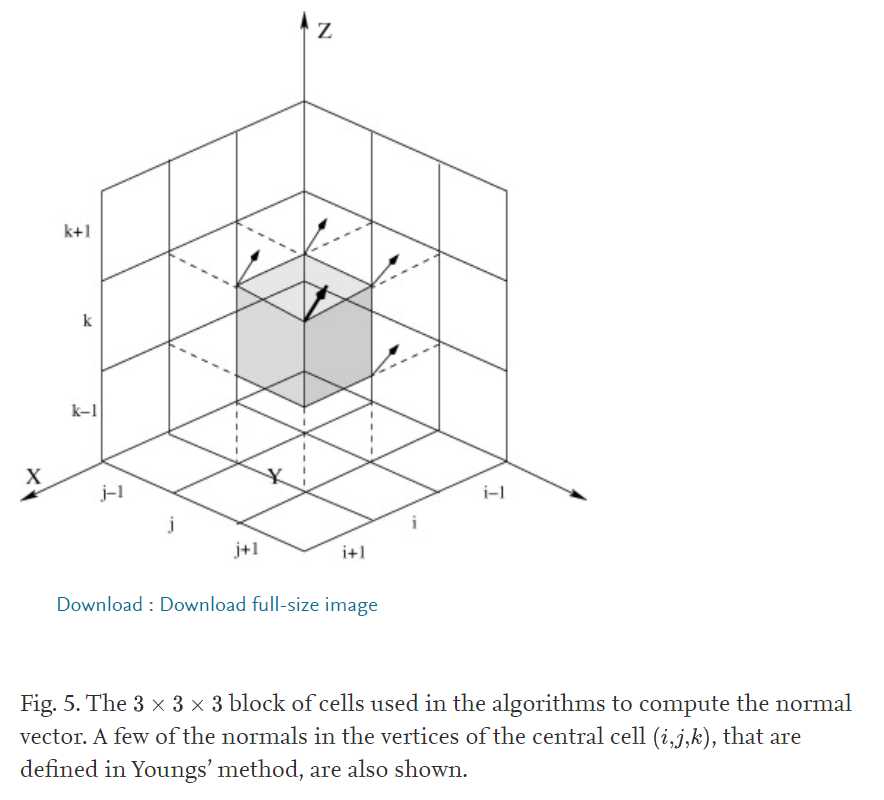
如以下的图5所示:
Youngs方法
我们定义C是体积分数的连续版本,也就是说C(\bm{x})意味着以x为中心的h^3格子中水的体积分数。那么可以发现,法向\bm{m}就是C的梯度:\bm{m}=-\nabla C.
在离散格式中,VOF场C定义在格子中心。那么我们可以在格子的八个角上用中心差分计算\bm{m}:
m_x=\frac{1}{h}(\overline{C}_i-\overline{C}_{i+1});
m_y=\frac{1}{h}(\overline{C}_j-\overline{C}_{j+1});
m_z=\frac{1}{h}(\overline{C}_k-\overline{C}_{k+1});
此处这些带横线的值都位于棱的中点,可以通过周围四个格子的VOF值取平均计算:
\overline{C}_i=(C_{i,j,k}+C_{i,j+1,k}+C_{i,j,k+1}+C_{i,j+1,k+1})/4.
这样可以在格子的八个顶点上算出八个法向,然后取它们的平均值,即为对格子法向的估计。
中心列方法
现在我们考虑对图5所示的3^3区域,固定z方向估计一个平面\mathrm{sgn}(m_z)z=m_xx+m_yy+\alpha.
这里的正负号\mathrm{sgn}可以用最底层和最顶层的C计算,而另外两个参数m_x和m_y由中心差分得出:
m_x=\frac{z_{i+1,j}-z_{i-1,j}}{2h}=\frac{1}{2}\left(\sum_{l=-1}^{1}C_{i+1,j,k+l}-\sum_{l=-1}^1C_{i-1,j,k+l}\right),
m_y=\frac{z_{i,j+1}-z_{i,j-1}}{2h}=\frac{1}{2}\left(\sum_{l=-1}^{1}C_{i,j+1,k+l}-\sum_{l=-1}^1C_{i,j-1,k+l}\right).
其实这就是上面讨论的高度函数法,即对每一列求和,然后对这个求和后的高度函数使用中心差分。
这样,中心列方法可以在x,y,z三个方向上给出三个估计。随后,我们用上一章描述的第二个判据从中选择一个方向,确定为平面的大致方向。然后,再用第一个判据比较中心列方法和Youngs方法所给出的两个估计,选择其中较好的那个。