参考文献:An accurate adaptive solver for surface-tension-driven interfacial flows
表面重建
计算截距
做advection的时候,认为每个格子里的界面都是一个平面(我们默认三维,二维就是直线)。也就是说有一个法向矢量\bm{m}和一个常数\alpha,那么这个格子的界面就是
\bm{m}\cdot\bm{x}=\alpha.
可以发现,如果这个格子的体积分数c(也就是VOF)和\bm{m}都已确定,那么\alpha就是唯一确定的。确定的方法类似marching cubes,即分类讨论平面和格子的各种相交情况,然后根据\alpha判断。文中对此没有详细讨论,但有两篇参考文献:
– Volume-of-Fluid Interface Tracking with Smoothed Surface Stress Methods for Three-Dimensional Flows
– Analytical Relations Connecting Linear Interfaces and Volume Fractions in Rectangular Grids
两篇的共同作者Ruben Scardovelli写了一个根据\bm{m}算\alpha的代码。
随后,文章假设这个给定\bm{m},联系c和\alpha的函数已知:c=\mathcal{V}(\bm{m},\alpha),反过来\alpha=\mathcal{V}^{-1}(\bm{m},c).
计算法向
现在,还有一个问题是计算\bm{m}. 大部分方法都需要一个“compact neighborhood”,比如规则网格下的3^3个格子,然后用有限差分或者最小化的方法估计\bm{m}. 但本文中采用的是自适应八叉树,须做一定的特殊处理。文章中描述了这里的特殊处理方法,大概是先找一个大格子,然后根据这个大格子生成一个虚拟的小格子用来计算,此处先不提。
在生成一个虚拟的规则网格之后,就采用规则网格上的算法计算\bm{m}。在这里叫做Mixed-Youngs-Centered (MYC),参考文献:Interface reconstruction with least-squares fit and split advection in three-dimensional Cartesian geometry
对流界面
接下来介绍如何对VOF做对流。这里有两个要点,第一是分离各方向上的对流,第二是根据先前介绍的,每格内估计出的界面去计算通量。
方向分离
文中给出了二维情况下的对流格式:
c_\star^{i,j}V_\star^{i,j}=c_{n-1/2}^{i,j}V_{n-1/2}^{i,j}+\phi_{n-1/2}^{i-1/2,j}-\phi_{n-1/2}^{i+1/2,j},
c_{n+1/2}^{i,j}V_{n+1/2}^{i,j}=c_\star^{i,j}V_\star^{i,j}+\phi_\star^{i,j-1/2}-\phi_\star^{i,j+1/2}.
也就是说,先对流x轴,再对流y轴。这个顺序每一个模拟时间步都应当交换,以免产生数值误差。
这里\phi的含义是每个面上的通量,我们随后再看。V的含义是“有效体积”。其原因是,本来每个格子的面积都是\Delta x^2(这里是二维),而且速度场无散,所以每个格子的总流入等于总流出,但单论x或y方向的总流入不一定等于总流出。所以,在单独进行x或y方向的对流时,可以认为速度场拥有一个临时的散度,那么每个格子所代表的控制体积也会被暂时改变。
V由下列公式给出:
V_\star^{i,j}=V_{n-1/2}^{i,j}+(u_n^{i-1/2,j}-u_n^{i+1/2,j})\Delta x\Delta t,
V_{n+1/2}^{i,j}=V_\star^{i,j}+(u_n^{i,j-1/2}-u_n^{i,j+1/2})\Delta x\Delta t.
由于速度场无散,所以V_{n+1/2}^{i,j}=V_{n-1/2}^{i,j}=\Delta x^2,也就是计算所有方向之后一个格子的体积仍然守恒。
面通量
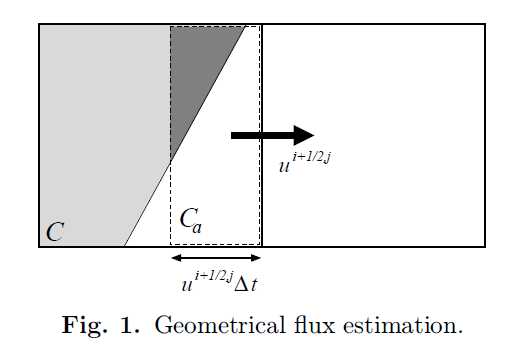
文中给出了一张示意图:
其中虚线框是根据速度计算出的,会通过界面的部分,斜线是格子中计算出来的表面,深灰色三角就是实际的体积通量。这个通量是采用某种几何方法计算出来的。