参考文献仍然是An accurate adaptive solver for surface-tension-driven interfacial flows
标准的2D规则网格曲率计算:
- 以欲计算曲率的格子(i,j,k)为中心,搞一个3\times 7或者7\times 3的stencil。具体是哪种取决于之前重建界面的时候MYC算出来的法向朝哪个方向。
- 在这个stencil里面把每一列的VOF值相加,得到高度函数y=h(x)或者x=h(y).
- 使用有限差分计算曲率\kappa=\frac{h”}{(1+h’^2)^{3/2}}.
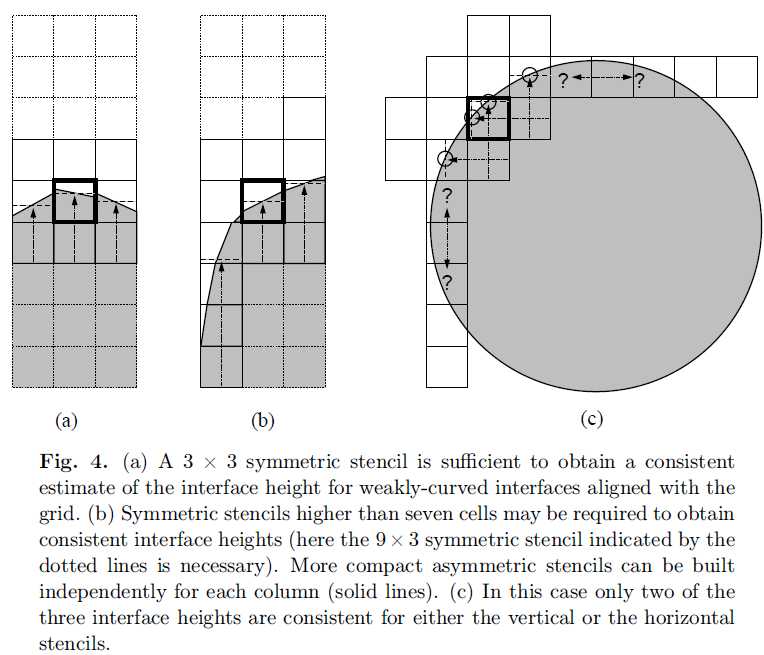
这样的问题是3\times 7这样死板的格子大小无法适应所有情况,如下面的图4:
图4.a这种情况根本就不需要7格高的stencil,其实3\times 3就够了。而图4.b这种情况却需要9格高的stencil才能完成计算。图4.c这种情况问题更大,不管取哪个方向,都会有一列的数据无效。
有一种方法是在局部使用非对称的stencil。比如说4.b里面,左边一列取4格,中间取3格,右边取6格。如下列算法:
其中C是一个格子坐标(i,j,k),c是VOF场c^{i,j,k}.这个算法写的比较绕,讲人话就是:先不断向上走(这个‘上’由输入参数top定义),直到找到第一个包含液-气界面的格子作为“顶”;再反过来向下找到一个包含液-气界面的“底”,把顶和底之间所有的VOF值加起来作为高度H。
写得这么绕的主要原因是,它需要检查这个高度是否合法。合法的意思就是说,“顶”再往上一格必须是纯气体,而“底”再往下一格必须是纯液体,否则就不合法,算法报错。这个往上一格,往下一格的特殊判断在算法里是用微操while循环实现的,所以很绕。
还有一点值得注意:只要起始格不是纯液体,那它自己就是“顶”;同样只要它不是纯气体它自己就是“底”。所以这个算法看似有两个方向,实际只会去搜索其中的一个。
在定义了这个表面高度函数Interface height之后,作者就定义了一个基于高度函数的曲率算法:
这里的意思就是说,假设我们选定x+为表面的朝向,那么就在y-z平面上看(i,j,k)的八个邻居,如果这八个邻居都能被Interface heighth函数给出合法的高度,那就用这个高度场算曲率。否则,就返回所有合法的界面点。合法的界面点的含义,比如说(i,j,k)有一个邻居(i,j+1,k),从它的格子中心开始,在x方向上可能找到某个界面上的点(x,jh,kh),h是格子边长,这就是一个合法的界面点。这里2.a的描述有一些模糊,我认为其实就是在平面上找邻居的意思。
获得这些合法的界面点之后,就可以用它们去拟合一个二次曲面,如下面的算法6所示:
这里还有一点需要注意,就是第一步说的是独立的界面点的个数。两个界面点\bm{a},\bm{b}独立的判据是|\bm{a}-\bm{b}|\geq h,这样保证这个最小二乘是一个well-condition问题。解最小二乘只需要求解一个6\times 6(三维)的线性方程组,所以时间开销并不大。
一般来说,高度函数和最小二乘这两招就够用了,但在一些特别极端的情况下,独立的界面点个数不够,连最小二乘也算不出来。这种情况下,就把周围3\times 3\times 3范围内,所有界面格子的界面重心取出来做最小二乘。如果还不行,那就说明大概率是一个退化的表面,直接把曲率置为0.
总的过程如算法7:
简单来说就是,先挨个尝试三个方向,如果有一个行就用它,如果都不行,就把三次计算出来的界面点合起来拟合。如果拟合不了再用算重心的方法。
最后还有一个小细节:因为我们用的是MAC网格,所以力是加在面上的,但是曲率是在格子上算的,那么就需要给出一个面上的曲率。文中的方法是:如果两个邻居格子都是界面格,就取二者曲率的平均。否则,就取有界面的那个格子的曲率值。






你写得非常清晰明了,让我很容易理解你的观点。