单向耦合
如果固体足够小,就可以忽略固体对流体的作用力,只考虑流体对固体的作用力。
固体受到的力分为两种:压力和粘性力。在固体非常小的时候,粘性力占主导,某点处的粘性力等于粘性张量乘以法向,总的受力就是:
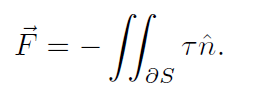
这里S代表固体的体积,法向指向固体外部。由于是单向耦合,因此不在固体表面应用无滑移边界条件,也就不能直接把流体的粘性张量拿来用。那怎么办呢?理论上讲,固体周围应该有边界层,应该拿边界层内的速度场算粘性张量,但边界层的流场问题还没有解决。因此书中就搞了一个简单的式子:
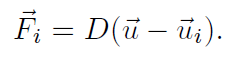
这里面F_i是i号固体 (非常小,近似粒子) 受到的粘性力/拖曳力,u是流体的速度场,u_i是i号固体的速度。D应当和流体的动力粘度成正比,可能根据每个固体的直径、截面积而改变。有时候甚至可以搞个非线性的,让D和u-u_i的模长成正比。
对于薄片状固体,有可能会约束速度的法向分量和固体相同,只在切向上加一个很小(甚至可能是零)的粘性力。
粘性力对固体产生的总力矩是:
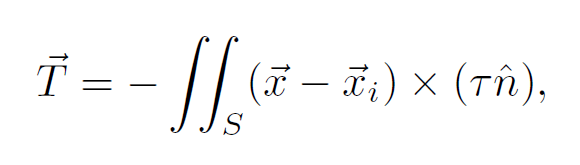
其中x_i是i号固体的重心。和前面类似,没有确切公式,同样给一个简单的:
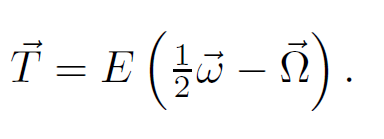
其中[latex]\Omega[/latex]是固体的角速度,[latex]\omega[/latex]是流体的旋度。E也是自己调,它可以是个矩阵。
压力的形式则简单一些:
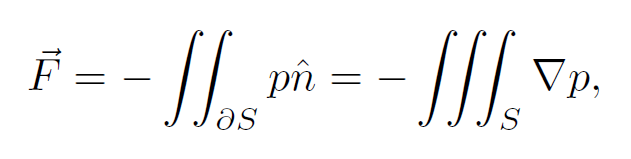
如果固体足够小,直接在其重心处计算[latex]\nabla p[/latex],然后乘以体积就可以了。
压力产生的总力矩是:
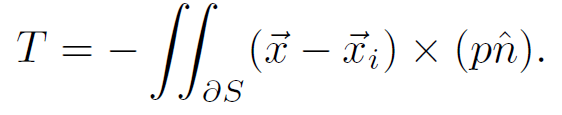
如果p足够平滑(接近于常数或者线性函数),这个积分的结果就可以忽略。这里注意:对于静水,压强在水面处并不平滑,因为水面上方空气都是0,但水下就是线性的,所以一半浮在水面上的物体会受到压力矩。对于这种情况,就需要对水下部分做积分(或者估算)了。
弱耦合
如果固体和流体能互相影响,那么就需要设法同时模拟二者。一种常见的做法叫做弱耦合(weak coupling)。这种方法是:交替进行流体步和固体步。最简单的算法如下:
1、流体对流步,更新固体位置和方向。
2、把非耦合的力加在流体和固体的速度场上(例如重力,内部弹性力)。
3、求解流体的压力方程,并据此修正流体速度,使之满足无散条件,固定固体速度,在其边界上对流体施加固壁边界条件。
4、根据上面求得的流体压强、碰撞、接触等,更新固体速度。
当然刻意弄得更复杂,比如多交替几次流体/固体步。但是弱耦合的本质不变:算流体步(求解压力方程)的时候假定固体速度不变,算固体步的时候假定流体压强不变。
其中,固定固体算流体就相当于流体加边界条件,在此不赘述。而固定流体算固体,实际就是计算固体受到的力和力矩,如之前单向耦合中所述。只要mesh足够细,例如和[latex]\Delta x[/latex]在同一量级上,那么可以直接做数值积分,比如说把三角形面片中间的压强乘以面积。粘性力也可以类似这么做。
但在一些情况下,数值积分可能不好操作,比如绳子这样的细长物体。这时候,可以把面积分转化成体积分,例如总压力:
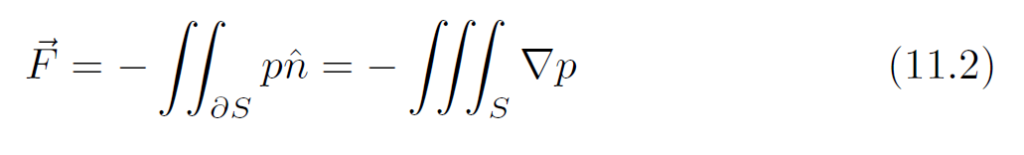
总力矩:
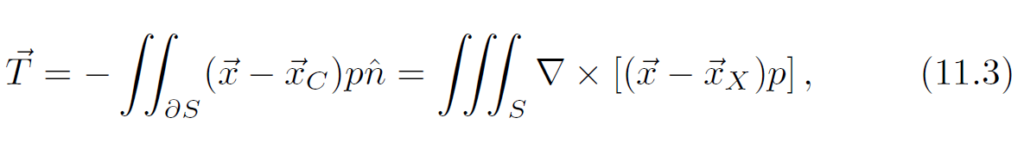
其中[latex]x_C[/latex]是重心。体积分可以由若干网格上的值加权求和得到。
有若干文章,如:[Takahashi et al. 02, Guendelman et al. 05]采用了这种方法。这种做法在软件工程上有优势(模块分离),但是有一些问题。例如,如果初始状态是一个固体一动不动地漂浮在水面上,那么固体的速度会在第2步中增加[latex]\Delta t\vec{g}[/latex],随后在第3步中,求解器会把这个速度作为边界条件,那么在完成速度校正后,流体的速度将非零。最终,压强场并未抵消固体的速度,固体会下沉一点,流体开始运动。这样的误差和时间步大小成正比,减小时间步可以降低误差,但计算开销会变大。
浸没边界法(Immersed Boundary Method)
浸没边界法是一个稍强一点的算法(可以看经典文章[Peskin 02])。这个算法赋予流体压力求解器一些“余量”,来改变固体速度。方法是暂时假装固体也是流体(但密度不同)。它不是简单地把固体速度作为求解流体压强的边界条件,而是把固体的质量和速度加到流体格子上,并在整个计算域内求解压强。每个节点处都有流体和固体的权值,加权确定平均密度和平均速度(这种做法和[Guendelman et al.05]类似)。
一种与此相关的方法是[Carlson et al. 04]提出的,他们在求解压强时,假设固体的密度和流体相等,然后在另一步中单独添加浮力。该文章没有在固体表面上施加压力,而是直接把固体占据的所有格子的速度平均起来,得到固体的速度。如果流体和固体的密度差别不太大,这种方法效果就很好。
对于无粘流体,把固体和流体速度做平均,可能会产生数值耗散,因为在固体边界上为滑移边界条件,流体固体速度可以不同。而做平均相当于无滑移边界条件,让流体和固体速度相等。在这种情况下,建议把流体的切向速度外推(extrapolate)到固体格子里,只对固体的法向速度做平均。对于非常薄的固体(例如布料),这种做法就变得很简单,因为固体太薄就不需要外推了,把法向/切向速度分开即可。
相比前面的弱耦合法,浸没边界法能解决一些问题,但仍然不能处理所有情况。例如,在模拟一个静止的,漂浮在水中的固体时,结果仍然很奇怪,因为在流体的压力求解器看来,固体是流体表面一个形状奇特的波。
一般稀疏矩阵
在讲解强耦合(同时借固体和流体)之前,我们先简单介绍稀疏矩阵,在之前章节的基础上进行扩展,因为我们先前所用的稀疏矩阵储存格式不适用于固体。
储存稀疏矩阵有几种可选的数据结构。我们关注的是行压缩(compressed sparse row/CSR)格式。在CSR里,每一行都用一个数组表示,数组中包含这一行的全部非零值,和它们对应的列编号。我们使用两个版本的CSR,其一是动态版本(这样构建矩阵时,能迅速添加非零元素),其二是静态版本(做PCG效果更好)。
动态CSR里面,每一行的数组分开储存,并且记录其长度。为了支持动态插入,我们可以额外申请一些空间,在这些空间用尽后,再申请两倍大小的空间,这和C++ STL vector用的方法类似。另外,人们通常把每个数组内部按照列坐标排序,这样查询某项和把两个稀疏矩阵相加都快得多。
但是PCG的核心操作是系数矩阵乘以稠密向量,如果拿动态CSR做乘法,效率会变低,因为每一行可能会分散在不同的内存块中,导致缓存命中率极差。因此,在使用动态CSR建好矩阵后,我们应当把它转换成静态CSR。在静态CSR里只有三个矩阵,保证所有非零元素在内存中连续:
- 一个浮点数组value,包含一列一列排序后的所有非零元素。
- 一个整型数组colindex,和value长度相同,包含value中相应元素的列坐标。
- 一个整型数组rowstart,长度为n+1(假设矩阵大小为n*n),描述在value或colindex矩阵中,每一列从哪里开始。这个数组的最后一个元素是整个矩阵中的非零元素个数,它代表了最后一行的结尾。
把动态CSR转为静态CSR需要花费一定时间,不过这段时间一般是值得的,因为它大大优化了PCG中矩阵乘向量的效率,使之接近先前提到的,基于网格的储存法。
我们之前使用的,基于网格储存矩阵的方法,针对对称矩阵进行优化,只储存上/下三角阵,从而省却了一半的空间。不过这个优化对于CSR并不值得,因为它让矩阵操作变得极为复杂。

静态CSR乘稠密向量的操作很简单,见图11.1.但我们还需要把不完全Cholesky预处理子(incomplete Cholesky preconditioner)和相应的三角阵求解搬到CSR上。一般而言,先前章节中做的假设(只需要计算对角元素,然后重用非对角元素)并不成立。此外,改进版不完全Cholesky分解不能使用先前所述的循环顺序。在CSR中,计算[latex]R=L^T[/latex]更自然一些。
总之,我们需要根据如下条件,确定标准版Cholesky分解的不完全因子(regular incomplete factor):
- R是上三角矩阵,若[latex]A_{i,j}=0[/latex]则应同时[latex]R_{i,j}=0[/latex]
- 若 [latex]A_{i,j}\neq 0[/latex] ,则应有[latex](R^T R)_{i,j}=A_{i,j}[/latex].
至于改进版Cholesky分解的不完全因子,则应满足如下条件:
- R是上三角矩阵,若[latex]A_{i,j}=0[/latex]则应同时[latex]R_{i,j}=0[/latex]
- 若[latex]A_{i,j}\neq 0[/latex]且i<j,则应有[latex](R^T R)_{i,j}=A_{i,j}[/latex].
- 每一行的和[latex]\Sigma_j (R^T R)_{i,j}[/latex]和A每一行的和[latex]\Sigma_j A_{i,j}[/latex]相等。


我们不深入解释如何使用CSR格式。不过,图11.2是构造R的伪代码(参数和之前相同),图11.3演示了如何通过求解R和[latex]R^T[/latex],使用预处理子。
强耦合
对于刚体和无粘流体的耦合问题,强耦合(strong coupling)是目前被研究得最透彻的方法。这是本章介绍的最后一种方法。接下来我们先给出连续形式的方程,然后再把它们离散化。
首先我们对刚体定义一些符号:
- [latex]\vec{X}[/latex]是刚体重心。
- [latex]\vec{V}[/latex]是刚体平动速度。
- [latex]\vec{\Omega}[/latex]是角速度。
- [latex]\vec{L}[/latex]是角动量。
- [latex]m[/latex]是质量。
- [latex]I[/latex]是转动惯量。
(可以把它轻易扩展到多个刚体的情况)。根据先前讨论的,流体压力赋予刚体的总受力和总力矩,刚体的更新方程如下:
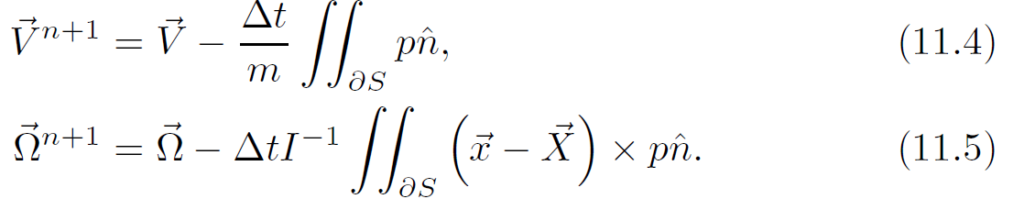
刚体上某点[latex]\vec{x}[/latex]的速度为:
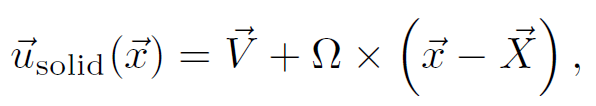
在求解压力方程的时候,它可以作为边界条件:
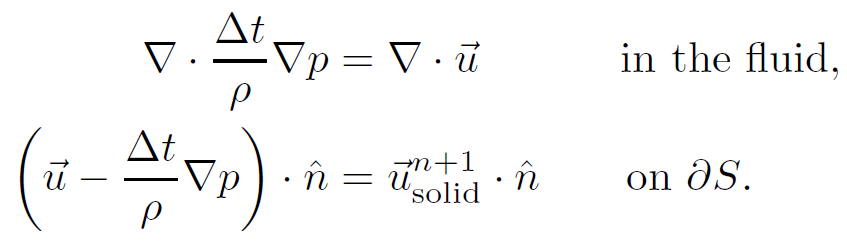
另外,在流体-气体的边界,应该施加自由边界条件p=0.
此处补充一点。在边界上,把[latex](\vec{V},\vec{\Omega})[/latex]映射至法向速度场的线性算子,等于在边界上把压强映射至固体总受力和总力矩的线性算子的伴随算子(对于矩阵而言,就是转置)。从上边的式子中看去,这不很显然,但可以被证明。这个性质决定了,在离散化之后,我们的压力方程会是一个对称矩阵。
[Batty et al.07]文中给出了一个更简单的方程组。我们使用方程(11.4)和(11.5)更新固体,但并不使用上文中说的边界条件。为了简化问题,我们以最小能量原则建立压力方程:压强场应当使得动能最小化。注意刚体的动能是[latex]\frac{1}{2}m||\vec{V}||^2+\frac{1}{2}\vec{\Omega}^TI\vec{\Omega}[/latex].
接下来我们来离散化这个变分方程。我们在之前的弱耦合一节中已经讨论过,如何计算固体受压力的影响(总受力和总力矩)。下面我们只需要明确地构建一个稀疏矩阵J,使得用J乘以包含全部格点压强值的向量,就能得到受力和力矩。根据方程(11.2),我们可以得到对应总受力的前三行。例如,总受力的x分量,[latex]F_1[/latex]如下:
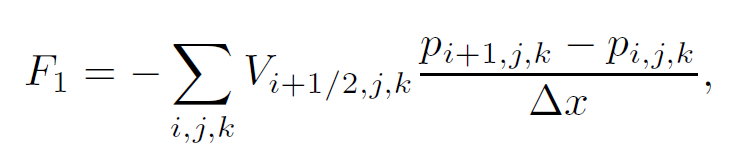
其中,[latex]V_{i+1/2,j,k}[/latex]是u-格子[latex](i+1/2,j,k)[/latex]中固体的体积。因此我们有
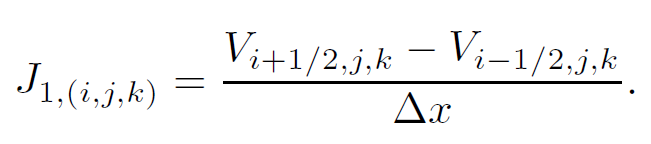
类似地,对应总受力y和z分量的后两行分别为:
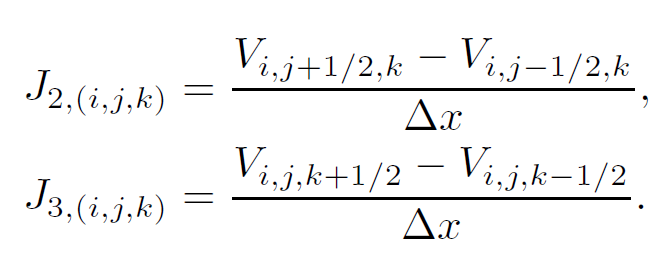
根据方程(11.3),我们可以得到J中对应总力矩的后三行。x分量[latex]T_1[/latex]的连续形式如下:
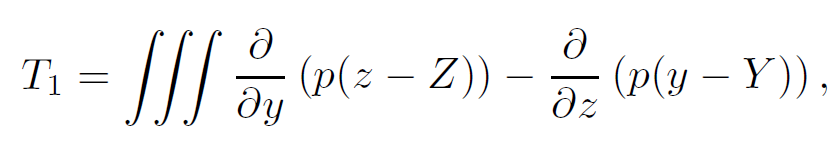
其中,固体的重心是[latex]\vec{X}=(X,Y,Z)[/latex].
上式可以简化为
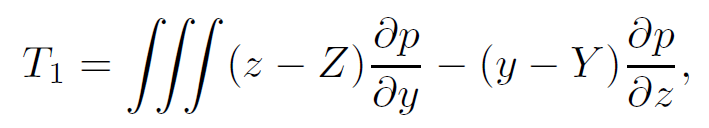
离散近似为:
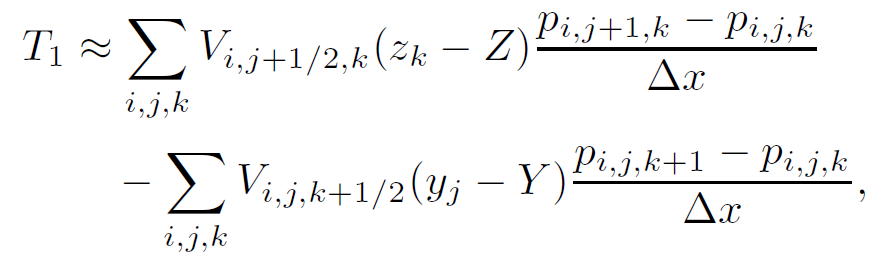
其中[latex]x_i,y_j,z_k[/latex]为[latex](i,j,k)[/latex]格中心的坐标。由此可以推导出J的第四行(力矩的x分量):
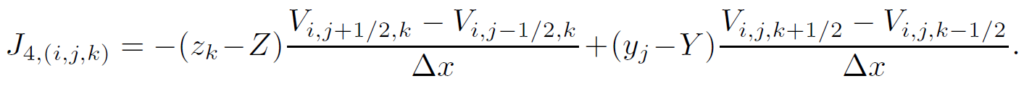
以及后两行(力矩的y,z分量):
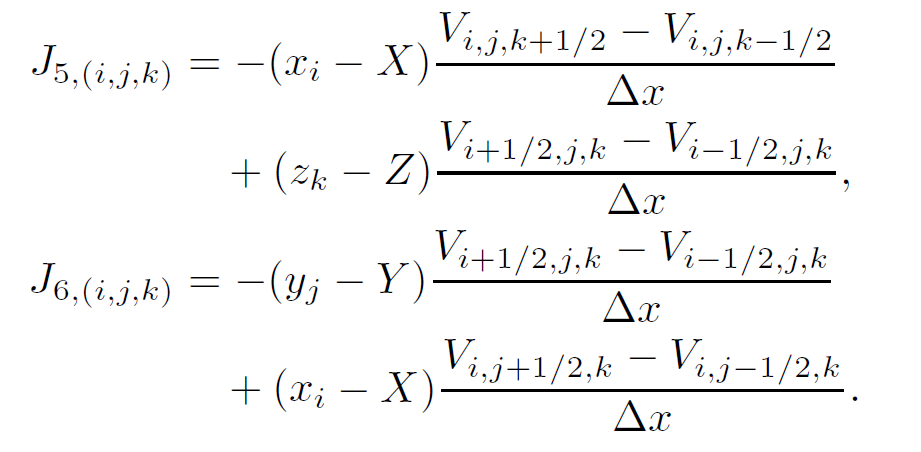
在固体边界之外,相邻格子的V值之差都是零,所以J是一个稀疏矩阵。它只有在固体边界附近才有非零列。
为了保持一致性,可以使用同样的V值计算固体的转动惯量,这样一来,完全浸没水中的固体就能完美地保持静止漂浮。但是,除此特定情况,这种做法大概没什么必要,我们把具体推导作为练习,留给有兴趣的读者。
为方便起见,我们把固体的平动速度[latex]\vec{V}[/latex]和角速度[latex]\vec{\Omega}[/latex]拼成一个六维向量[latex]\vec{U}[/latex].同样,把质量和转动惯量拼成一个6*6的矩阵M:
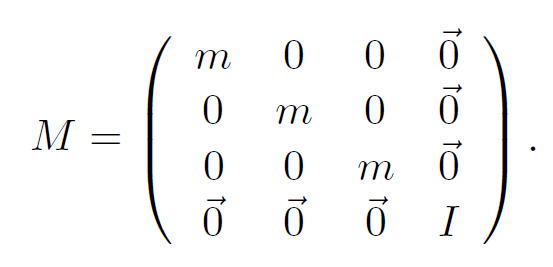
那么刚体的动能就是[latex]\frac{1}{2}\vec{U}^TM\vec{U}[/latex],压力修正步是[latex]\vec{U}^{n+1}=\vec{U}+\Delta tM^{-1}Jp[/latex].
最后,我们来讨论离散最小化。把动能对压强求导得到:
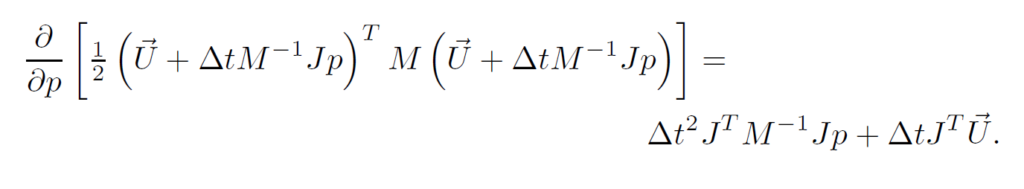
把它和第四章末推导出的流体动能合起来,进行恰当的放缩使量纲一致(除以[latex]\Delta t[/latex],用真实体积值代替体积分数),最终的结果是左端矩阵多了[latex]\Delta tJ^TM^{-1}J[/latex],右端多了[latex]-J^T\vec{U}[/latex].
这正是我们需要处理一般系数矩阵的原因:[latex]\Delta tJ^TM^{-1}J[/latex]并不对应网格结构。实际上,它在边界附近格子的对应列处有着稠密子矩阵。如果你对线性代数感兴趣,可以发现它的秩至多为6,并且一定是对称半正定矩阵——所以PCG仍然能用。但是稠密子矩阵的性质可能会导致求解性能下降,可以在分解后插入一些额外项来避免这点。PCG涉及到矩阵乘稠密向量的运算,这个操作可以通过把[latex]J^TM^{-1}Js[/latex]换成[latex]J^T(M^{-1}(J^Ts))[/latex]来加速。由于秩不超过6,因此计算预处理子代价不大。
大块固体可能会和许多格子重叠,这是一个值得考虑的问题:需要用大量内存储存它们,并且PCG可能会变得很慢,由于稠密子矩阵太大。一种可能的方案是在压力求解中,把新的固体速度[latex]\vec{U}^{n+1}[/latex]作为辅助变量,得到一个稍大但更稀疏的矩阵:
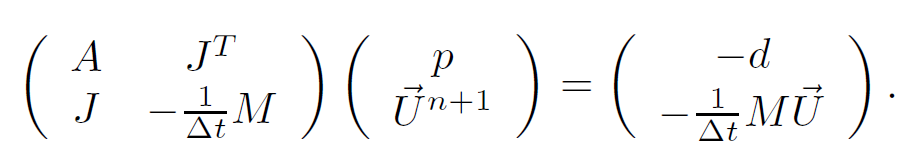
这仍然是一个对称矩阵,但它可能是不定的,因此不能使用PCG。不过,对这种矩阵的求解也是一个经典问题,它有时会被叫做“鞍点”(saddle-point)矩阵(实际上,除去压力为常数的零空间,它应该是一个对称拟正定/symmetric quasi-definite矩阵),有专门的求解算法。例如,可以采用MINRES这样的迭代方法,结合形如[latex]LDL^T[/latex](L是单位对角阵/unit diagonal,D是对角阵,其中压强值的对应项为正,刚体的对应项为负)的不完全Cholesky预处理子。如果想了解求解此类矩阵的方法,可以去看[Benzi et al. 05]的综述文章。
另一个有趣的研究方向,是考虑如何把这种方法用于关节状固体的强耦合:例如,拉格朗日乘子法可以表述为最小化动能。摩擦力也可以这么做,但它的约束是不等式,这让最小化变得很复杂。
如果需要模拟软体,上面说的最小化能量算法就不够用了。在软体-流体耦合问题中,强耦合意味着把软体本身的隐式时间步和流体的压力求解结合起来。但是,隐式求解弹性力(最小化弹性势能)不能被简单地描述为,求解一个力,来最小化能量。在写作本书时,图形学领域只有[Chentanez et al.06]研究过这个问题。他们使用非结构化的四面体网格来离散化流体,在软体边界处网格的形状和软体一致。目前,还没有使用结构化网格和固体体积分数的方法。本章至此结束。
