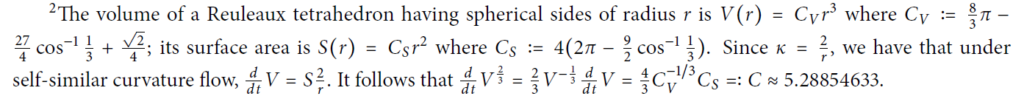3.10收敛性测试和数值验证
首先是每算例都做三组:
- 固定[latex]\epsilon[/latex],改变网格尺寸h,检查[latex]h\to 0[/latex]的收敛情况。
- 固定比例关系[latex]\epsilon=\alpha h[/latex],其中[latex]\alpha[/latex]为一常数,检查[latex]h\to 0[/latex]的收敛情况。
- 交换极限,先算一个[latex]\epsilon\to 0^+[/latex]的内极限,然后检查[latex]h\to 0[/latex]的收敛情况。
所有测试都是在规则正方形/立方体网格上完成的。
3.10.1二维基础测试
一个圆环以固定速度向外扩展。
一个正方形以固定速度向外扩展。
一个正方形以固定速度收缩。
一个圆环在表面张力的作用下减速收缩。
这些都可以和解析解做对比。
3.10.2二维分歧点
在表面张力下,T-junction逐步演化成Y-junction:
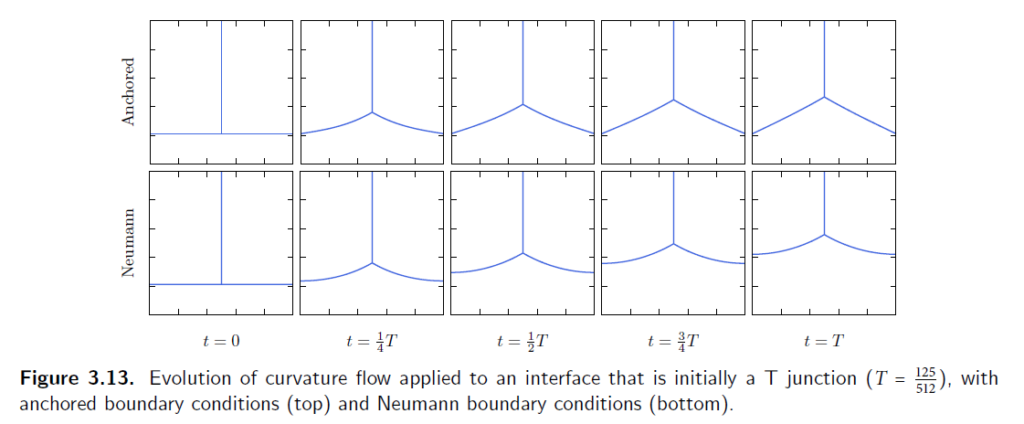
这个没有解析解,进行收敛性分析。
3.10.3二维von Neumann-Mullins定理
使用Young-Laplace定理,沿着二维泡泡单个cell表面积一圈分,得到其面积变化率:

也就是说单个cell面积变化仅与其边数有关,而且面积随时间的变化函数总是分段线性的。
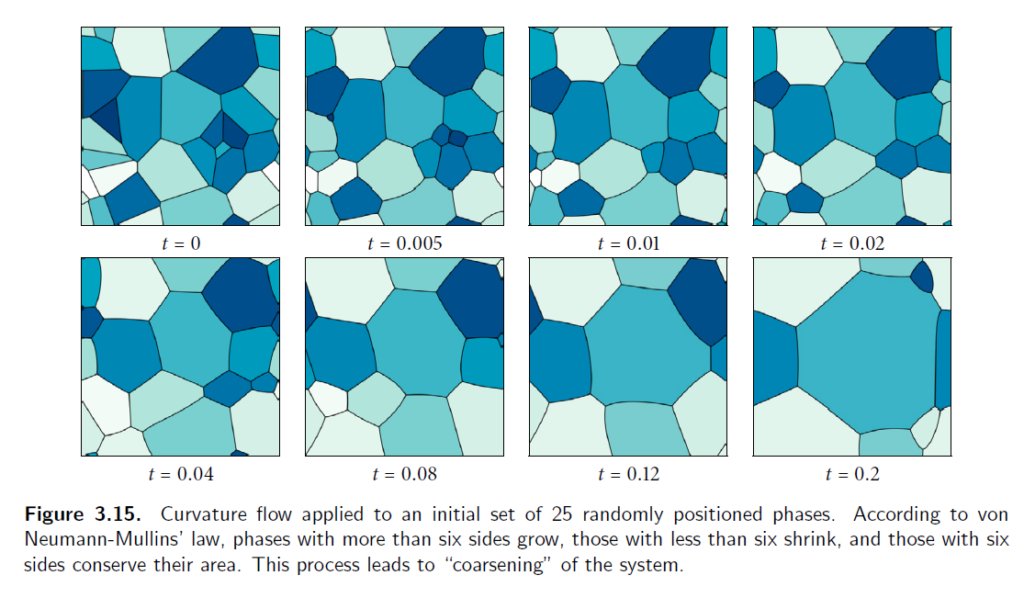
然后随机初始态算了一下,说这个符合von Neumann-Mullins定理,各不同边数cell的面积变化如下:
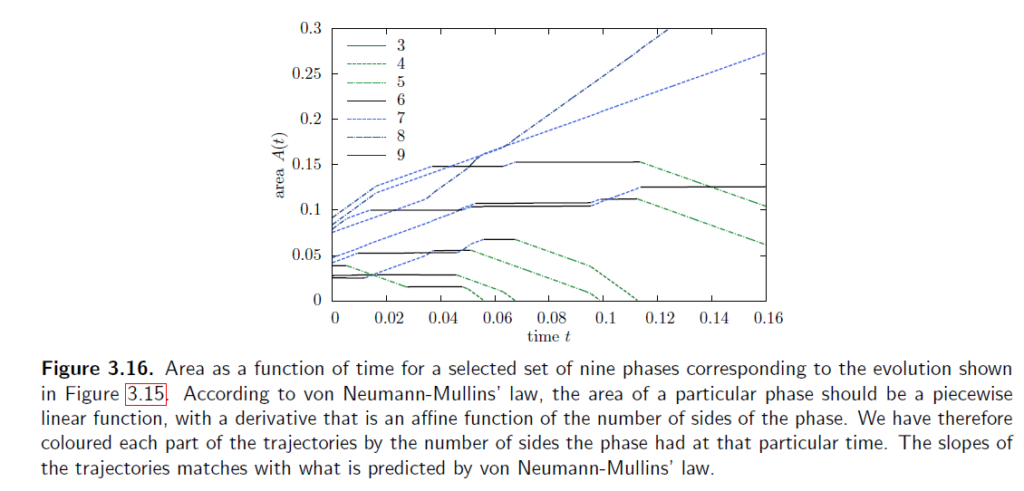
然后又算了一下各边数的收敛状况:
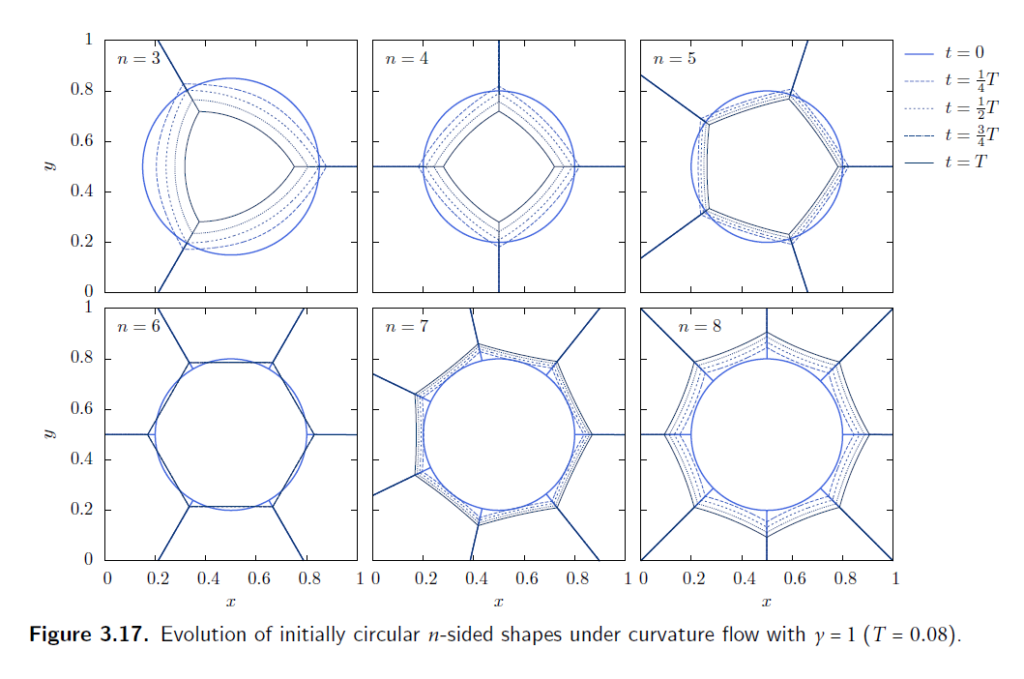
3.10.4三维分歧点
和二维的类似。
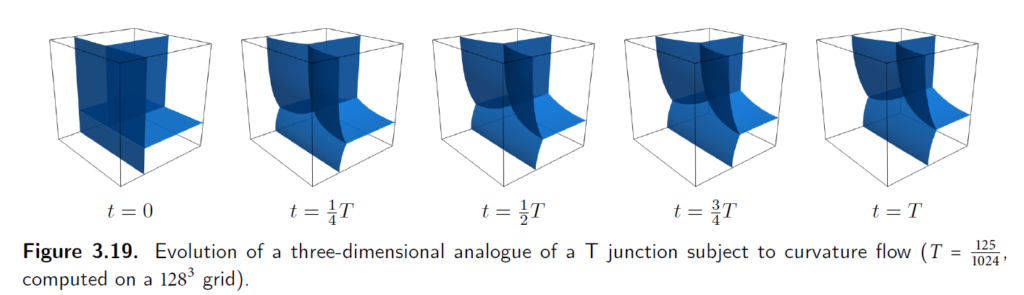
3.10.5三维von Neumann-Mullins定理
Reuleaux tetrahedron收缩。这个有解析解。
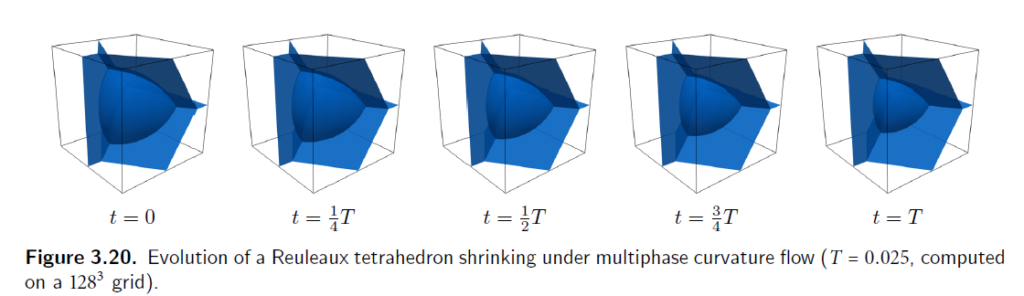
推导如下: