Method of Characterstics特征方法
Stable Fluids文章中使用特征方法解决Advection(对流)。
维基百科对特征方法的解释:
https://en.wikipedia.org/wiki/Method_of_characteristics
就是找一条让PDE成为ODE的线,沿着这条线解ODE,这样就搞定了原来的PDE问题。
看论文中的解释:
特征方法用来解这样的方程:
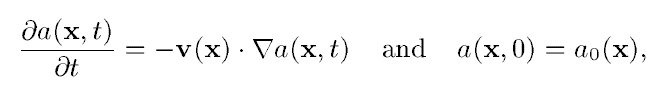
这个[latex]\frac{\partial a(\textbf{x},t)}{\partial t}+\textbf{v}(\textbf{x})\cdot\nabla a(\textbf{x},t)[/latex]其实就是随体导数。
然后论文定义[latex]\textbf{p}(\textbf{x}_0,t)[/latex]为速度场\textbf{v}的characterstics(特征),满足
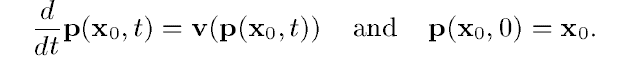
这个[latex]\textbf{p}(\textbf{x}_0,t)[/latex]的意思就是在时刻0时位于[latex]\textbf{x}_0[/latex]的这个流体点在[latex]t[/latex]跑到了什么地方。
定义![]()
为场a的“随体场”,也就是采取拉格朗日观点,定义它为0时刻在[latex]\textbf{x}_0[/latex]的流体点在t时刻的值。
上面说了,我们要解的方程相当于随体导数,那么[latex]\bar{a}[/latex]就是“随体场”,所以求解的直接就是它的时间导数
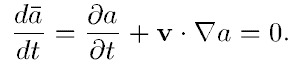
具体来说,在做Advection的时候,沿着流线(characterstic line)“上溯”一步即可。
边界条件
Jos Stam代码中的边界条件如下:
void set_bnd ( int N, int b, float * x )
{
int i;
for ( i=1 ; i<=N ; i++ ) {
x[IX(0 ,i)] = b==1 ? -x[IX(1,i)] : x[IX(1,i)];
x[IX(N+1,i)] = b==1 ? -x[IX(N,i)] : x[IX(N,i)];
x[IX(i,0 )] = b==2 ? -x[IX(i,1)] : x[IX(i,1)];
x[IX(i,N+1)] = b==2 ? -x[IX(i,N)] : x[IX(i,N)];
}
x[IX(0 ,0 )] = 0.5f*(x[IX(1,0 )]+x[IX(0 ,1)]);
x[IX(0 ,N+1)] = 0.5f*(x[IX(1,N+1)]+x[IX(0 ,N)]);
x[IX(N+1,0 )] = 0.5f*(x[IX(N,0 )]+x[IX(N+1,1)]);
x[IX(N+1,N+1)] = 0.5f*(x[IX(N,N+1)]+x[IX(N+1,N)]);
}
Stable Fluids采用的边界条件是Dirichlet边界条件,也就是:在边界处,速度场的法向分量为零。即,没有任何通量“穿过”边界。
在文章中,速度场的离散点分布如下:

注意这里的坐标是1~N.想要实现“法向为零”的边界条件怎么办呢?我们取边界上的一个点,算该点处的速度值时,会取“外面”的速度点:
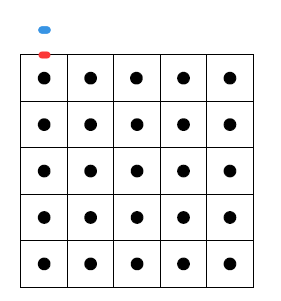
就像这样,红点的速度值是格子左上角黑点和格子外面蓝点的平均值。
那么,如果想让红点处速度的y分量为零,只需要把蓝点速度的y分量置为黑点速度的y分量的相反数即可。
蓝点的x分量呢?红点速度的x分量应当和黑点的x分量相同,那么蓝点的x分量也应该等于黑点的x分量。
最后,set_bnd函数的结尾四句是设置四个角的边界条件:
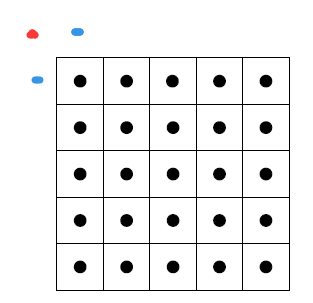
红点的速度是两个蓝点速度的平均值。原因是,例如我们考察y分量,令红点为y00:
y01=-y11
y10=y11
考虑到角上的速度应当为0,也就是说(y00+y01+y10+y11)/4=0,代入得到y00+y11=0,x的情况类似,也就是说红点的速度应该和黑点的速度恰好相反。
但是Jos Stam代码中,这个点的速度应该是0,原因有待实验。
Poisson Solver
在Stable Fluids里面,求解泊松方程的代码长这样:
void lin_solve ( int N, int b, float * x, float * x0, float a, float c )
{
int i, j, k;
for ( k=0 ; k<20 ; k++ ) {
FOR_EACH_CELL
x[IX(i,j)] = (x0[IX(i,j)] + a*(x[IX(i-1,j)]+x[IX(i+1,j)]+x[IX(i,j-1)]+x[IX(i,j+1)]))/c;
END_FOR
set_bnd ( N, b, x );
}
}
这是啥玩意呢?查了一圈发现,这玩意就是线性方程组的Jacobi Solver.看一眼维基百科:
https://en.wikipedia.org/wiki/Jacobi_method
注意,每次是“基于”对角元去更新解向量,这可以解释为什么更新的是x[i][j].
Jacobi Solver的条件是:对角元最大。这个怎么满足呢?把泊松方程离散化以后,就变成了类似拉普拉斯算子的玩意:
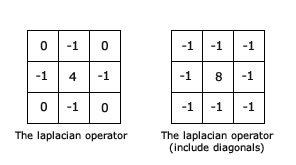
比方说一个大致长这样的算子,中间被加了好多次,可不就是最大了嘛。每个格子一个方程,自然对角线上的元素最大。

您好我最近也在读这篇论文,关于边界条件还是有点不太明白。为何黑色点处的速度等于红色蓝色相加取平均?红色和蓝色不应该是在同一个边界格子里吗
面中心节点和格子中心节点的区别吧?