2 运动方程
文中推导的是不可压缩弹性固体的方程。目标是让弹性方程看起来尽量像流体方程一样。
(q,r,s)是固体上的曲线坐标。X(q,r,s,t)是该固体质点在t时刻的位置。M(q,r,s)是质量密度。由能量密度函数E[X]定义固体材料性质。弹性力就是它的Frechet导数:

这里[latex]\wp[/latex]是小扰动的意思。[latex]\wp\mathbf{X}[/latex]的意思就是在X基础上的小扰动。类似地[latex]\wp E[/latex]就是对总能量的小扰动。
定义体积改变比例J:
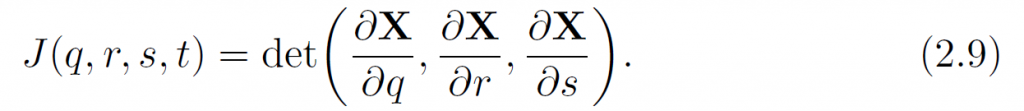
弹性固体材料不可压缩也就是:

根据最小作用量原理,物体运动应当最小化:

这个L是Lagrangian.而运动过程满足固体不可压方程(2.10)和初始/终止位置:
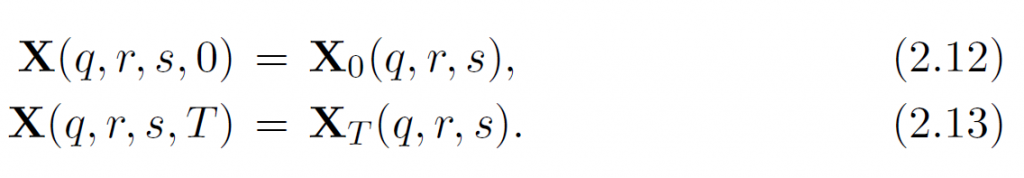
运动过程的Lagrangian一般是动能减去势能:
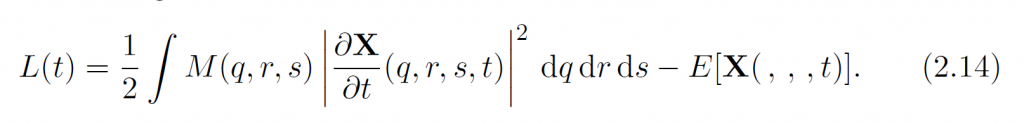
因此位移的能量最小化就是:
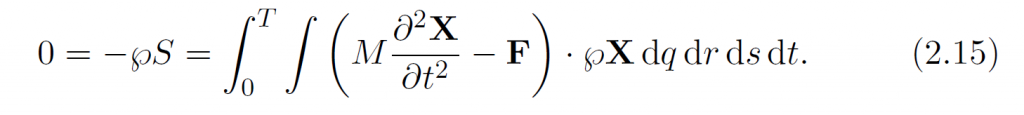
文中说:第一项是对t做分步积分而来。第二项需要用到F的定义,也就是弹性势能E的Frechet导数。不过看上去,这个的意思好像是,[latex]\wp\mathbf{X}[/latex]是对X做小扰动,那么[latex]\wp S[/latex]就是[latex]\wp L[/latex]的积分,计算方法就是L对X求导,然后乘以小扰动[latex]\wp\mathbf{X}[/latex](线性近似)。
定义Eularian速度场u,那么不可压缩方程就是[latex]\nabla\cdot\mathbf{u}=0[/latex].再由定义扰动v:
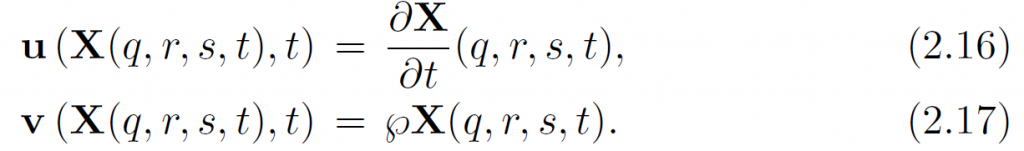
也就是说,u(x,t)是t时刻x处物质点的速度。v是该物质点的扰动(和静息状态相比)。
对Eularian速度u求物质导数:

进而有加速度:
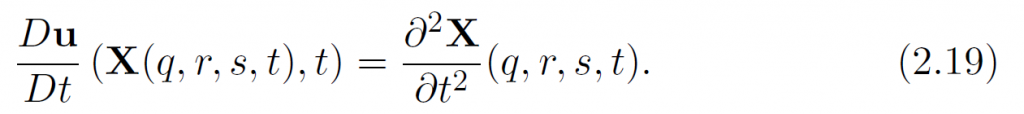
v虽然看上去是速度,但其实是位移。由于固体不可压,J应该保持不变。
令

那么[latex]\partial X/\partial a[/latex]是一个3*3矩阵。而

我们现在该式两端施加扰动算子。
有恒等式:
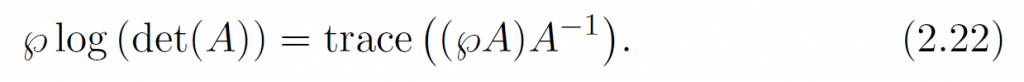
推导如下:
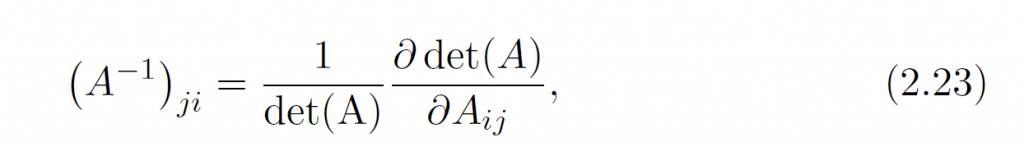
这个相当于是把[latex]A_{ij}[/latex]的cofactor(也就是伴随矩阵里的i,j项)写成[latex]\partial det(A)/\partial A_{ij}[/latex].
因此用全导数写出来就是:
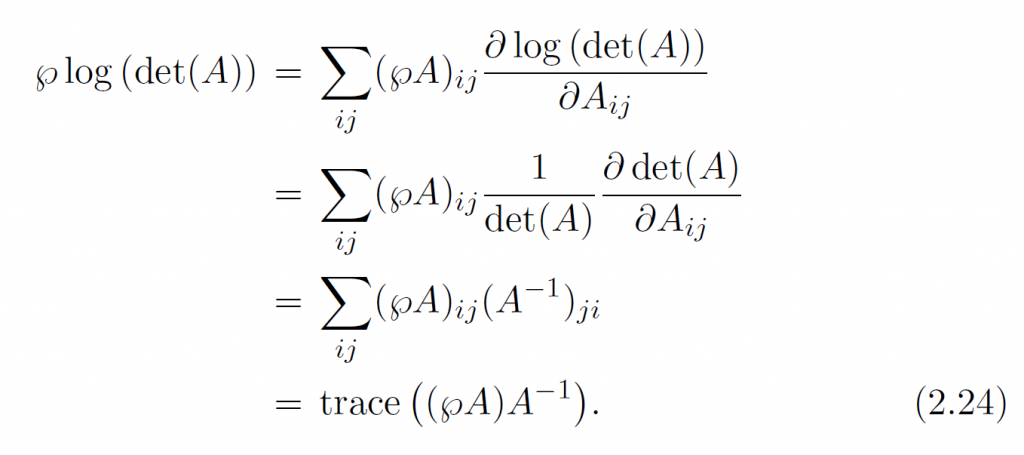
根据链式法则:

变换一下:
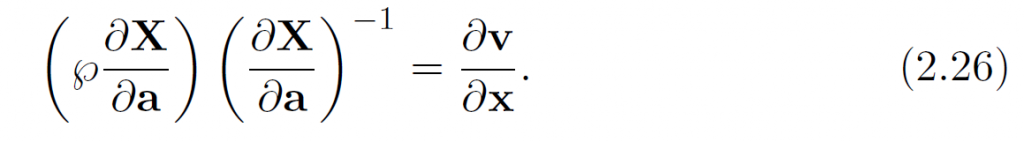
两边取trace:
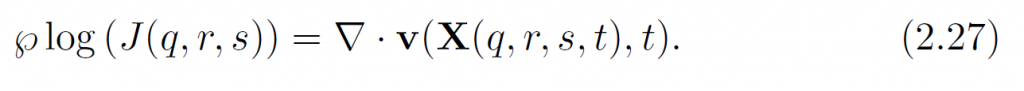
因此不可压缩方程等于:

这和Eularian速度的不可压缩方程类似:

使用Dirac函数可以得到:
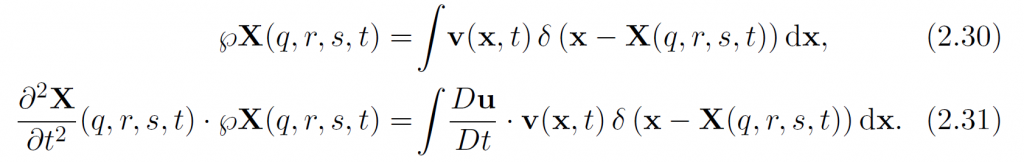
这个意思可以大致理解为[latex]\wp X(q,r,s,t)=v(x,t)[/latex].
然后代入刚才的最小能量条件(2.15):
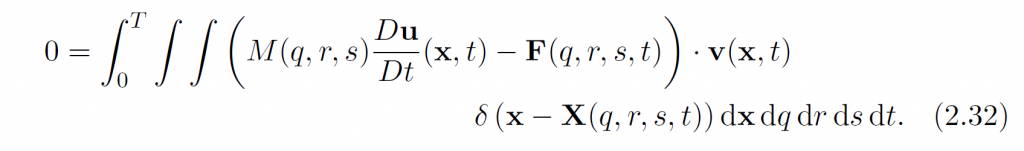
这里面质量M和弹性力密度F是Lagrangian的,但其他是Eularian的。为了把Lagrangian消掉,我们先定义Eularian量:
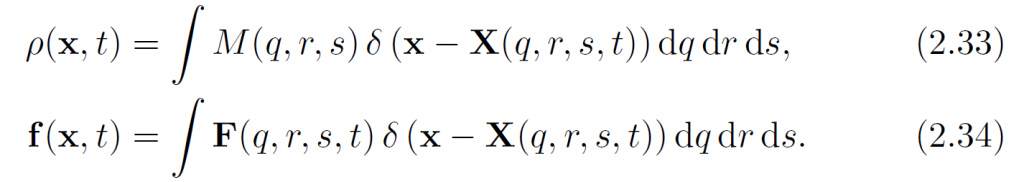
然后就可以把(2.32)写作:
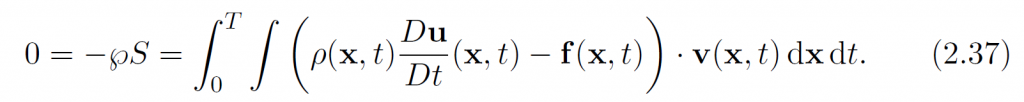
位移v满足v(x,0)=v(x,T)=0(注:这里没太明白)和无散条件[latex]\nabla\cdot\mathbf{v}=0[/latex].
这里使用Hodge分解:
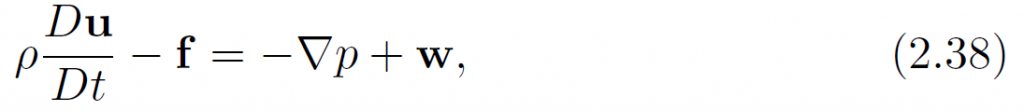
其中

下面证明w=0.设

要求[latex]\phi(0)=\phi(T)=0[/latex],且令(0,T)之间[latex]\phi(t)>0[/latex],那么(2.37)变为:
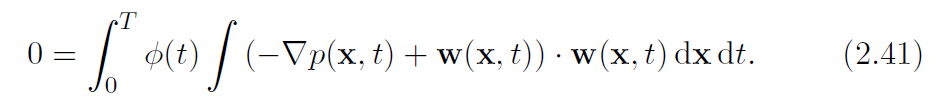
由于[latex]\nabla\cdot w=0[/latex],所以p那一项被消去了,剩下:
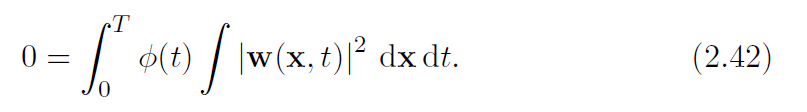
由于[latex]\phi[/latex]总为正,所以[latex]w=0[/latex].
然后再加上一个粘性项(像牛顿流体一样),整个不可压缩弹性固体的运动方程就是:
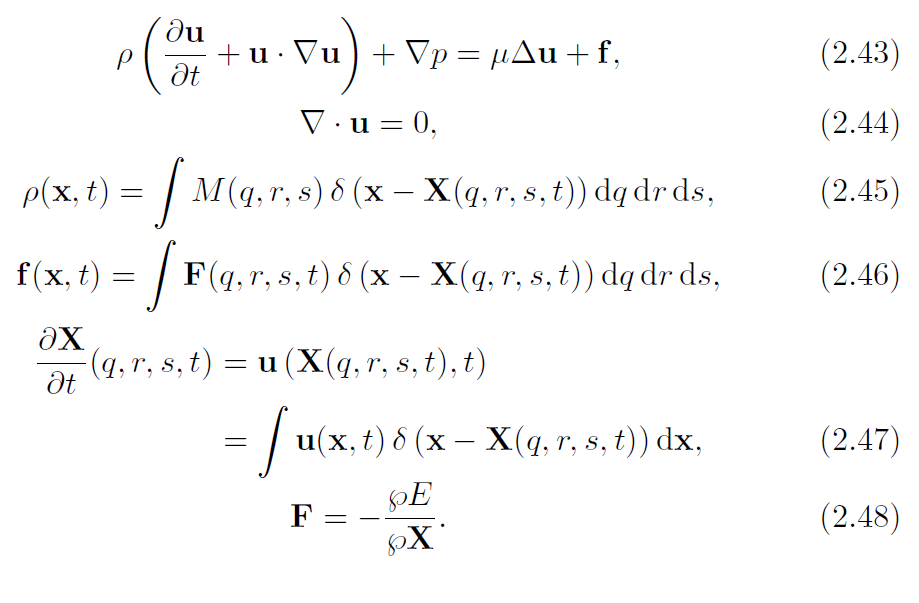
一定要注意,这实际上是固体的方程。等于是把用狄拉克函数把Lagrangian物理量转移到Eularian网格上,从而把固体方程写成了流体的形式。
一般来说流体还会有一个质量守恒方程:

也就是[latex]D\rho/Dt=0[/latex].这个可以从(2.44),(2.45),(2.47)推出:
(2.45)两侧对t求偏导得:
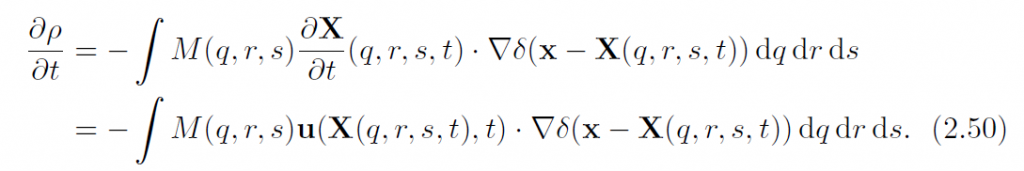
而(2.45)与u点积而得:
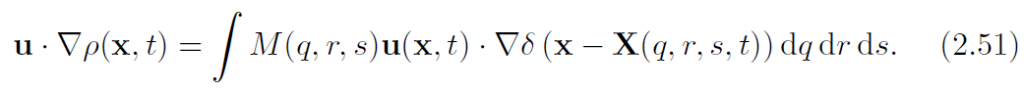
然后首先证明一下:
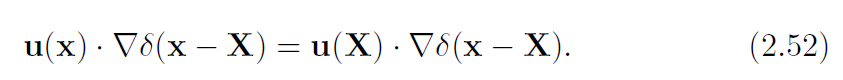
证明方法是,对于任意函数[latex]\phi[/latex]:
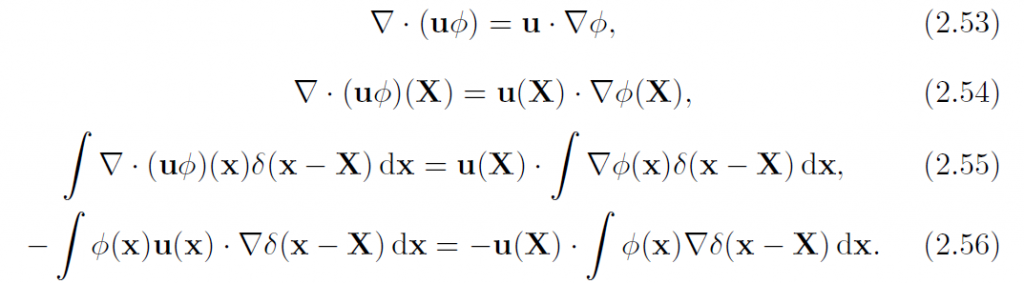
这对任意[latex]\phi[/latex]成立,所以(2.52)成立。这样就可以从(2.50),(2.51)推出(2.49).
3 流体和固体的交互
流体的方程其实跟前面列出的固体方程差不多。但是流体不涉及弹性势能函数E,它的Lagrangian弹性力[latex]\mathbf{F}=-\wp E/\wp\mathbf{X}[/latex]等于零,对应的Eularian值f也是零。
假设流体有固定密度[latex]\rho_0[/latex],用固体的“额外密度”[latex]\tilde{M}[/latex]代替Lagrangian密度M:
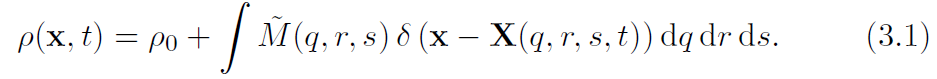
等于是密度减去它排开水的密度。这个额外密度有可能是负的,也就是固体比流体更轻。
对于浸没在流体中的表面,描述一个点只需要两个Lagrangian变量(r,s),那么交互方程就是:
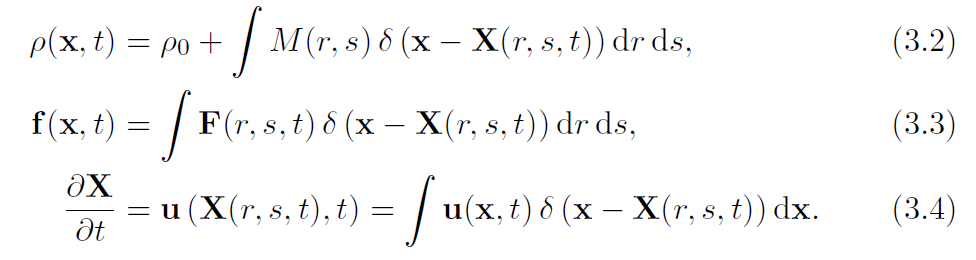
这里面,由于排开水的体积为零,所以额外密度等于密度。
这里的方程等价于那种带pressure jump的方程。证明可见Peskin and Printz(1993),Lai and Li(2001).
4 空间离散化
(待续)
